Assembly: ImslCS (in ImslCS.dll) Version: 6.5.0.0
 Syntax
Syntax
| C# |
|---|
[SerializableAttribute] public class ContingencyTable |
| Visual Basic (Declaration) |
|---|
<SerializableAttribute> _ Public Class ContingencyTable |
| Visual C++ |
|---|
[SerializableAttribute] public ref class ContingencyTable |
 Remarks
Remarks
Class ContingencyTable computes statistics associated with an
![]() contingency table. The function computes
the chi-squared test of independence, expected values, contributions to
chi-squared, row and column marginal totals, some measures of
association, correlation, prediction, uncertainty, the McNemar test for
symmetry, a test for linear trend, the odds and the log odds ratio, and
the kappa statistic (if the appropriate optional arguments are
selected).
contingency table. The function computes
the chi-squared test of independence, expected values, contributions to
chi-squared, row and column marginal totals, some measures of
association, correlation, prediction, uncertainty, the McNemar test for
symmetry, a test for linear trend, the odds and the log odds ratio, and
the kappa statistic (if the appropriate optional arguments are
selected).
Notation
Let ![]() denote the observed cell frequency in
the ij cell of the table and n denote the total count in
the table. Let
denote the observed cell frequency in
the ij cell of the table and n denote the total count in
the table. Let ![]() denote the predicted cell probabilities under the null hypothesis of
independence, where
denote the predicted cell probabilities under the null hypothesis of
independence, where ![]() and
and
![]() are the row and column marginal
relative frequencies. Next, compute the expected cell counts as
are the row and column marginal
relative frequencies. Next, compute the expected cell counts as
![]() .
.
Also required in the following are ![]() and
and
![]() for
for ![]() .
Let
.
Let ![]() denote the row and column response
of observation s. Then,
denote the row and column response
of observation s. Then, ![]() , or
-1, depending on whether
, or
-1, depending on whether ![]() , or
, or
![]() , respectively. The
, respectively. The
![]() are similarly defined in terms of the
are similarly defined in terms of the
![]() variables.
variables.
Chi-squared Statistic
For each cell in the table, the contribution to
![]() is given as
is given as
![]() . The Pearson chi-squared
statistic (denoted
. The Pearson chi-squared
statistic (denoted ![]() ) is computed as the sum
of the cell contributions to chi-squared. It has (r - 1) (c - 1)
degrees of freedom and tests the null hypothesis of independence, i.e.,
) is computed as the sum
of the cell contributions to chi-squared. It has (r - 1) (c - 1)
degrees of freedom and tests the null hypothesis of independence, i.e.,
![]() . The null
hypothesis is rejected if the computed value of
. The null
hypothesis is rejected if the computed value of
![]() is too large.
is too large.
The maximum likelihood equivalent of ![]() is computed as follows:
is computed as follows:
![]() is asymptotically equivalent to
is asymptotically equivalent to
![]() and tests the same hypothesis with the same
degrees of freedom.
and tests the same hypothesis with the same
degrees of freedom.
Measures Related to Chi-squared (Phi, Contingency Coefficient, and Cramer's V)
There are three measures related to chi-squared that do not depend on sample size:
Since these statistics do not depend on sample size and are large when
the hypothesis of independence is rejected, they can be thought of as
measures of association and can be compared across tables with different
sized samples. While both P and V have a range between 0.0
and 1.0, the upper bound of P is actually somewhat less than 1.0
for any given table (see Kendall and Stuart 1979, p. 587). The
significance of all three statistics is the same as that of the
![]() statistic, which is contained in the
ChiSquared property.
statistic, which is contained in the
ChiSquared property.
The distribution of the ![]() statistic in
finite samples approximates a chi-squared distribution. To compute the
exact mean and standard deviation of the
statistic in
finite samples approximates a chi-squared distribution. To compute the
exact mean and standard deviation of the ![]() statistic, Haldane (1939) uses the multinomial distribution with fixed
table marginals. The exact mean and standard deviation generally differ
little from the mean and standard deviation of the associated
chi-squared distribution.
statistic, Haldane (1939) uses the multinomial distribution with fixed
table marginals. The exact mean and standard deviation generally differ
little from the mean and standard deviation of the associated
chi-squared distribution.
Standard Errors and p-values for Some Measures of Association
In Columns 1 through 4 of statistics, estimated standard errors and asymptotic p-values are reported. Estimates of the standard errors are computed in two ways. The first estimate, in Column 1 of the return matrix from the Statistics property, is asymptotically valid for any value of the statistic. The second estimate, in Column 2 of the array, is only correct under the null hypothesis of no association. The z-scores in Column 3 of statistics are computed using this second estimate of the standard errors. The p-values in Column 4 are computed from this z-score. See Brown and Benedetti (1977) for a discussion and formulas for the standard errors in Column 2.
Measures of Association for Ranked Rows and Columns
The measures of association, ![]() , P, and
V, do not require any ordering of the row and column categories.
Class ContingencyTable also computes several measures of
association for tables in which the rows and column categories
correspond to ranked observations. Two of these tests, the
product-moment correlation and the Spearman correlation, are correlation
coefficients computed using assigned scores for the row and column
categories. The cell indices are used for the product-moment
correlation, while the average of the tied ranks of the row and column
marginals is used for the Spearman rank correlation. Other scores are
possible.
, P, and
V, do not require any ordering of the row and column categories.
Class ContingencyTable also computes several measures of
association for tables in which the rows and column categories
correspond to ranked observations. Two of these tests, the
product-moment correlation and the Spearman correlation, are correlation
coefficients computed using assigned scores for the row and column
categories. The cell indices are used for the product-moment
correlation, while the average of the tied ranks of the row and column
marginals is used for the Spearman rank correlation. Other scores are
possible.
Gamma, Kendall's ![]() , Stuart's
, Stuart's
![]() , and Somers' D are measures of
association that are computed like a correlation coefficient in the
numerator. In all these measures, the numerator is computed as the
"covariance" between the
, and Somers' D are measures of
association that are computed like a correlation coefficient in the
numerator. In all these measures, the numerator is computed as the
"covariance" between the ![]() variables and
variables and
![]() variables defined above, i.e., as follows:
variables defined above, i.e., as follows:
Recall that ![]() and
and ![]() can take values -1, 0, or 1. Since the product
can take values -1, 0, or 1. Since the product
![]() only if
only if
![]() and
and ![]() are both 1
or are both -1, it is easy to show that this "covariance" is twice the
total number of agreements minus the number of disagreements, where a
disagreement occurs when
are both 1
or are both -1, it is easy to show that this "covariance" is twice the
total number of agreements minus the number of disagreements, where a
disagreement occurs when ![]() .
.
Kendall's ![]() is computed as the correlation
between the
is computed as the correlation
between the ![]() variables and the
variables and the
![]() variables (see Kendall and Stuart 1979, p.
593). In a rectangular table
variables (see Kendall and Stuart 1979, p.
593). In a rectangular table ![]() , Kendall's
, Kendall's
![]() cannot be 1.0 (if all marginal totals are
positive). For this reason, Stuart suggested a modification to the
denominator of
cannot be 1.0 (if all marginal totals are
positive). For this reason, Stuart suggested a modification to the
denominator of ![]() in which the denominator
becomes the largest possible value of the "covariance." This maximizing
value is approximately
in which the denominator
becomes the largest possible value of the "covariance." This maximizing
value is approximately ![]() , where
m = min (r, c). Stuart's
, where
m = min (r, c). Stuart's ![]() uses this
approximate value in its denominator. For large
uses this
approximate value in its denominator. For large
![]() .
.
Gamma can be motivated in a slightly different manner. Because the
"covariance" of the ![]() variables and the
variables and the
![]() variables can be thought of as twice the
number of agreements minus the disagreements, 2(A - D), where
A is the number of agreements and D is the number of
disagreements, Gamma is motivated as the probability of agreement minus
the probability of disagreement, given that either agreement or
disagreement occurred. This is shown as
variables can be thought of as twice the
number of agreements minus the disagreements, 2(A - D), where
A is the number of agreements and D is the number of
disagreements, Gamma is motivated as the probability of agreement minus
the probability of disagreement, given that either agreement or
disagreement occurred. This is shown as
![]() .
.
Two definitions of Somers' D are possible, one for rows and a
second for columns. Somers' D for rows can be thought of as the
regression coefficient for predicting ![]() from
from
![]() . Moreover, Somer's D for rows is the
probability of agreement minus the probability of disagreement, given
that the column variable,
. Moreover, Somer's D for rows is the
probability of agreement minus the probability of disagreement, given
that the column variable, ![]() , is not 0. Somers'
D for columns is defined in a similar manner.
, is not 0. Somers'
D for columns is defined in a similar manner.
A discussion of all of the measures of association in this section can be found in Kendall and Stuart (1979, p. 592).
Measures of Prediction and Uncertainty
Optimal Prediction Coefficients: The measures in this section do not require any ordering of the row or column variables. They are based entirely upon probabilities. Most are discussed in Bishop et al. (1975, p. 385).
Consider predicting (or classifying) the column for a given row in the table. Under the null hypothesis of independence, choose the column with the highest column marginal probability for all rows. In this case, the probability of misclassification for any row is 1 minus this marginal probability. If independence is not assumed within each row, choose the column with the highest row conditional probability. The probability of misclassification for the row becomes 1 minus this conditional probability.
Define the optimal prediction coefficient
![]() for predicting columns from rows as
the proportion of the probability of misclassification that is
eliminated because the random variables are not independent. It is
estimated by
for predicting columns from rows as
the proportion of the probability of misclassification that is
eliminated because the random variables are not independent. It is
estimated by
where m is the index of the maximum estimated probability in the
row ![]() or row margin
or row margin
![]() . A similar coefficient is defined
for predicting the rows from the columns. The symmetric version of the
optimal prediction
. A similar coefficient is defined
for predicting the rows from the columns. The symmetric version of the
optimal prediction ![]() is obtained by summing
the numerators and denominators of
is obtained by summing
the numerators and denominators of ![]() and
and ![]() then dividing. Standard errors
for these coefficients are given in Bishop et al. (1975, p. 388).
then dividing. Standard errors
for these coefficients are given in Bishop et al. (1975, p. 388).
A problem with the optimal prediction coefficients
![]() is that they vary with the marginal
probabilities. One way to correct this is to use row conditional
probabilities. The optimal prediction
is that they vary with the marginal
probabilities. One way to correct this is to use row conditional
probabilities. The optimal prediction ![]() coefficients are defined as the corresponding
coefficients are defined as the corresponding
![]() coefficients in which first the row (or
column) marginals are adjusted to the same number of observations. This
yields
coefficients in which first the row (or
column) marginals are adjusted to the same number of observations. This
yields
where i indexes the rows, j indexes the columns, and
![]() is the (estimated) probability of column
j given row i.
is the (estimated) probability of column
j given row i.
is similarly defined.
Goodman and Kruskal ![]() : A second kind of
prediction measure attempts to explain the proportion of the explained
variation of the row (column) measure given the column (row) measure.
Define the total variation in the rows as follows:
: A second kind of
prediction measure attempts to explain the proportion of the explained
variation of the row (column) measure given the column (row) measure.
Define the total variation in the rows as follows:
Note that this is 1/(2n) times the sums of squares of the
![]() variables.
variables.
With this definition of variation, the Goodman and Kruskal
![]() coefficient for rows is computed as the
reduction of the total variation for rows accounted for by the columns,
divided by the total variation for the rows. To compute the reduction in
the total variation of the rows accounted for by the columns, note that
the total variation for the rows within column j is defined as follows:
coefficient for rows is computed as the
reduction of the total variation for rows accounted for by the columns,
divided by the total variation for the rows. To compute the reduction in
the total variation of the rows accounted for by the columns, note that
the total variation for the rows within column j is defined as follows:
The total variation for rows within columns is the sum of the
![]() variables. Consistent with the usual methods in
the analysis of variance, the reduction in the total variation is given as
the difference between the total variation for rows and the total
variation for rows within the columns.
variables. Consistent with the usual methods in
the analysis of variance, the reduction in the total variation is given as
the difference between the total variation for rows and the total
variation for rows within the columns.
Goodman and Kruskal's ![]() for columns is similarly
defined. See Bishop et al. (1975, p. 391) for the standard errors.
for columns is similarly
defined. See Bishop et al. (1975, p. 391) for the standard errors.
Uncertainty Coefficients: The uncertainty coefficient for rows is the increase in the log-likelihood that is achieved by the most general model over the independence model, divided by the marginal log-likelihood for the rows. This is given by the following equation:
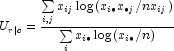
The uncertainty coefficient for columns is similarly defined. The
symmetric uncertainty coefficient contains the same numerator as
![]() and
and ![]() but
averages the denominators of these two statistics. Standard errors for
U are given in Brown (1983).
but
averages the denominators of these two statistics. Standard errors for
U are given in Brown (1983).
Kruskal-Wallis: The Kruskal-Wallis statistic for rows is a one-way analysis-of-variance-type test that assumes the column variable is monotonically ordered. It tests the null hypothesis that no row populations are identical, using average ranks for the column variable. The Kruskal-Wallis statistic for columns is similarly defined. Conover (1980) discusses the Kruskal-Wallis test.
Test for Linear Trend: When there are two rows, it is possible to test for a linear trend in the row probabilities if it is assumed that the column variable is monotonically ordered. In this test, the probabilities for row 1 are predicted by the column index using weighted simple linear regression. This slope is given by
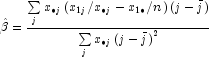
where
is the average column index. An asymptotic test that the slope is 0 may then be obtained (in large samples) as the usual regression test of zero slope.
In two-column data, a similar test for a linear trend in the column probabilities is computed. This test assumes that the rows are monotonically ordered.
Kappa: Kappa is a measure of agreement computed on square tables only. In the kappa statistic, the rows and columns correspond to the responses of two judges. The judges agree along the diagonal and disagree off the diagonal. Let
denote the probability that the two judges agree, and let
denote the expected probability of agreement under the independence
model. Kappa is then given by ![]() .
.
McNemar Tests: The McNemar test is a test of symmetry in a square
contingency table. In other words, it is a test of the null hypothesis
![]() . The multiple
degrees-of-freedom version of the McNemar test with r (r - 1)/2
degrees of freedom is computed as follows:
. The multiple
degrees-of-freedom version of the McNemar test with r (r - 1)/2
degrees of freedom is computed as follows:
The single degree-of-freedom test assumes that the differences,
![]() , are all in one direction. The
single degree-of-freedom test will be more powerful than the multiple
degrees-of-freedom test when this is the case. The test statistic is
given as follows:
, are all in one direction. The
single degree-of-freedom test will be more powerful than the multiple
degrees-of-freedom test when this is the case. The test statistic is
given as follows:
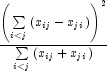
The exact probability can be computed by the binomial distribution.