Regression Analysis Classes
The Business Analysis Module provides classes for performing analyses of overall model significance for linear and logistic regressions. These classes are
RWLinearRegressionANOVA,
RWLogisticFitAnalysis, and
RWLinearRegressionFTest. Let’s discuss these in more detail in the following sections.
Class RWLinearRegressionANOVA
Class
RWLinearRegressionANOVA may be used to conduct an analysis of variance for a linear regression. The quantities calculated include: overall F statistic, residual sum of squares, regression sum of squares, degrees of freedom for the regression and residuals, mean square error, coefficient of determination, and adjusted coefficient of determination.
Using the class is fairly easy. You simply specify a linear regression object, either at construction time or via the member function setLinearRegression(), and query the object for the various ANOVA quantities. Here is a simple example:
RWGenMat<double> predictorMatrix; // Values for the predictor
// variables
RWMathVec<double> observationVector; // Values for the dependent
// variable
.
.
.
RWLinearRegression lr( predictorMatrix, observationVector );
if ( lr.fail() ) // Make sure the parameters were calculated
{
cerr << "linear regression calculation failed" << endl;
}
else
{
// Construct an ANOVA object from the linear regression model
// and print the results.
RWLinearRegressionANOVA lrANOVA( lr );
cout << "F statistic: " << lrANOVA.FStatistic() << endl;
cout << "F statistic p-value: " << lrANOVA.FStatisticPValue()
<< endl;
cout << "F statistic critical value: "
<< lrANOVA.FStatisticCriticalValue(.05) << endl;
cout << "mean square residual " << lrANOVA.meanSquareResidual() << endl;
cout << "mean square regression " << lrANOVA.meanSquareRegression() << endl;
cout << "Rsquare: " << lrANOVA.RSquare() << endl;
cout << "adjusted Rsquare: " << lrANOVA.adjRSquare()
<< '\n' << endl;
}
.
.
.
Class RWLogisticFitAnalysis
Class
RWLogisticFitAnalysis is similar to class
RWLinearRegression, which was described above. To use
RWLogisticFitAnalysis, you specify a logistic regression, either at construction time or via the
setLogisticRegression() member function, and query the object for the various fit analysis quantities. The following example demonstrates the procedure.
RWLogisticRegression model;
.
.
.
RWLogisticFitAnalysis logfit(model);
cout << "Pearson statistic: " << logfit.PearsonStatistic() << endl;
cout << "Pearson statistic p-value: " <<
logfit.PearsonStatisticPValue() << endl;
cout << "Pearson statistic 10% critical value: " <<
logfit.PearsonStatisticCriticalValue(0.10) << endl;
cout << "Pearson statistic degrees of freedom: " <<
logfit.PearsonStatisticDegreesOfFreedom() << endl;
cout << "Predictor data groups for Pearson statistic: " <<
logfit.predictorDataGroups() << endl;
cout << endl;
cout << "HL statistic: " << logfit.HLStatistic() << endl;
cout << "HL statistic p-value: " << logfit.HLStatisticPValue() <<
endl;
cout << "HL statistic 10% critical value: " <<
logfit.HLStatisticCriticalValue(0.10) << endl;
cout << "HL statistic degrees of freedom: " <<
logfit.HLStatisticDegreesOfFreedom() << endl;
cout << "Bin counts for predictions: " <<
logfit.HLStatisticOutputHistogram() << endl;
cout << "Bin counts for predictions associated \n
with positive observations: "
<< logfit.HLStatisticPosObsHistogram() << endl;
cout << endl;
.
.
.
Class RWLinearRegressionFTest
Suppose that we have the linear regression model:
Y = β0 + β1x1 + β2x2 + β3x3 + β4x4
and we want to test the hypothesis Ha:β2 = β4 = 0 and the hypothesis Hb:β1 = β3.
We can express each of these hypotheses in the matrix form
Aβ =
c, where
β = [
β0,
β1,
β2,
β3,
β4],
c = 0,
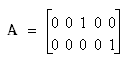
for H
a, and A = [0 1 0 –1 0] for H
b.
The
RWLinearRegressionFTest class can be used for testing hypotheses of the above form
Aβ =
c, where
β is the vector of
p parameters for the linear regression model,
A is a known
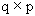
matrix of rank
q, and
c is a known
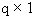
vector. The following is an example that tests both types of hypotheses.
int main()
{
RWGenMat<double> predictorMatrix; // Predictor variable values
RWMathVec<double> observationVector; // Dependent variable values
double significanceLevel = .05;
if ( !getDataFromFile("crime.dat", predictorMatrix,
observationVector) )
{
return 0;
}
RWLinearRegression lr( predictorMatrix, observationVector );
RWLinearRegressionFTest FTest( lr );
// Test that B3 = B4.
RWGenMat<double> A( 1, lr.numParameters(), 0.0 );
RWMathVec<double> c( 1, 0.0 );
A(0,3) = 1.0;
A(0,4) = -1.0;
FTest.setHypothesis( A, c );
cout << "F Test for H0 B3 = B4\n" << endl;
cout << " F statistic value: " << FTest.FStatisticValue() <<
endl;
cout << " F statistic p-value: " << FTest.FStatisticPValue() <<
endl;
cout << " Critical value: " <<
FTest.criticalValue(significanceLevel) << '\n' << endl;
if ( FTest.reject(significanceLevel) )
{
cout << "Reject H0 at significance level " << significanceLevel
<< endl;
}
else
{
cout << "Fail to reject H0 at significance level " <<
significanceLevel << endl;
}
return 0;
}
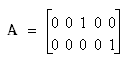 for Ha, and A = [0 1 0 –1 0] for Hb.
for Ha, and A = [0 1 0 –1 0] for Hb.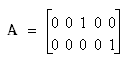 for Ha, and A = [0 1 0 –1 0] for Hb.
for Ha, and A = [0 1 0 –1 0] for Hb.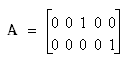 for Ha, and A = [0 1 0 –1 0] for Hb.
for Ha, and A = [0 1 0 –1 0] for Hb.