- java.lang.Object
-
- com.imsl.math.BSpline
-
- All Implemented Interfaces:
- Serializable, Cloneable
- Direct Known Subclasses:
- BsInterpolate, BsLeastSquares
public abstract class BSpline extends Object implements Serializable, Cloneable
BSpline represents and evaluates univariate B-splines.B-splines provide a particularly convenient and suitable basis for a given class of smooth ppoly functions. Such a class is specified by giving its breakpoint sequence, its order k, and the required smoothness across each of the interior breakpoints. The corresponding B-spline basis is specified by giving its knot sequence
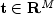 . The specification rule is as follows: If the class is to have
all derivatives up to and including the j-th derivative continuous across
the interior breakpoint
. The specification rule is as follows: If the class is to have
all derivatives up to and including the j-th derivative continuous across
the interior breakpoint 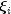 , then the number
, then the number
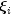 should occur k - j - 1 times in the
knot sequence. Assuming that
should occur k - j - 1 times in the
knot sequence. Assuming that 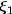 and
and 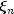 are the endpoints of the interval of interest, choose the first
k knots equal to
are the endpoints of the interval of interest, choose the first
k knots equal to 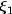 and the last k
knots equal to
and the last k
knots equal to  . This can be done because the
B-splines are defined to be right continuous near
. This can be done because the
B-splines are defined to be right continuous near 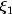 and left continuous near
and left continuous near 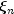 .
.
When the above construction is completed, a knot sequence
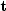 of length M is generated, and there are m: =
M-k B-splines of order k, for example
of length M is generated, and there are m: =
M-k B-splines of order k, for example 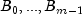 , spanning the ppoly functions on the interval with the
indicated smoothness. That is, each ppoly function in this class has a
unique representation
, spanning the ppoly functions on the interval with the
indicated smoothness. That is, each ppoly function in this class has a
unique representation 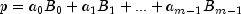 as a linear combination of B-splines. A B-spline is a
particularly compact piecewise polynomial function.
as a linear combination of B-splines. A B-spline is a
particularly compact piecewise polynomial function. 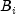 is a nonnegative function that is nonzero only on the interval
is a nonnegative function that is nonzero only on the interval
![[{bf t}_i,{bf t}_{i+k}]](eqn_1932.png) . More precisely, the support
of the i-th B-spline is
. More precisely, the support
of the i-th B-spline is ![left[ t_i,t_{i+k}right]](eqn_1933.png) . No
piecewise polynomial function in the same class (other than the zero
function) has smaller support (i.e., vanishes on more intervals) than a
B-spline. This makes B-splines particularly attractive basis functions since
the influence of any particular B-spline coefficient extends only over a few
intervals.
. No
piecewise polynomial function in the same class (other than the zero
function) has smaller support (i.e., vanishes on more intervals) than a
B-spline. This makes B-splines particularly attractive basis functions since
the influence of any particular B-spline coefficient extends only over a few
intervals.
-
-
Field Summary
Fields Modifier and Type Field and Description protected double[]coefThe B-spline coefficient array.protected double[]knotThe knot array of length n + order, where n is the number of coefficients in the B-spline.protected intorderOrder of the spline.
-
Constructor Summary
Constructors Constructor and Description BSpline()
-
Method Summary
Methods Modifier and Type Method and Description doublederivative(double x)Returns the value of the first derivative of the B-spline at a point.double[]derivative(double[] x, int ideriv)Returns the value of the derivative of the B-spline at each point of an array.doublederivative(double x, int ideriv)Returns the value of the derivative of the B-spline at a point.double[]getKnots()Returns a copy of the knot sequence.SplinegetSpline()Returns aSplinerepresentation of the B-spline.doubleintegral(double a, double b)Returns the value of an integral of the B-spline.doublevalue(double x)Returns the value of the B-spline at a point.double[]value(double[] x)Returns the value of the B-spline at each point of an array.
-
-
-
Field Detail
-
coef
protected double[] coef
The B-spline coefficient array.
-
knot
protected double[] knot
The knot array of length n + order, where n is the number of coefficients in the B-spline.
-
order
protected int order
Order of the spline.
-
-
Method Detail
-
derivative
public double derivative(double x)
Returns the value of the first derivative of the B-spline at a point.- Parameters:
x- adoublespecifying a point at which the derivative is to be evaluated- Returns:
- a
doublecontaining the value of the first derivative of the B-spline at the pointx
-
derivative
public double[] derivative(double[] x, int ideriv)Returns the value of the derivative of the B-spline at each point of an array.- Parameters:
x- adoublearray of points at which the derivative is to be evaluatedideriv- anintspecifying the derivative to be computed. If zero, the function value is returned. If one, the first derivative is returned, etc.- Returns:
- a
doublearray containing the value of the derivative the B-spline at each point of the arrayx
-
derivative
public double derivative(double x, int ideriv)Returns the value of the derivative of the B-spline at a point.- Parameters:
x- adoublespecifying a point at which the derivative is to be evaluatedideriv- anintspecifying the derivative to be computed. If zero, the function value is returned. If one, the first derivative is returned, etc.- Returns:
- a
doublecontaining the value of the derivative of the B-spline at the pointx
-
getKnots
public double[] getKnots()
Returns a copy of the knot sequence.- Returns:
- a
doublearray containing a copy of the knot sequence.
-
getSpline
public Spline getSpline()
Returns aSplinerepresentation of the B-spline.- Returns:
- a
Splinerepresentation of theBSpline
-
integral
public double integral(double a, double b)Returns the value of an integral of the B-spline.- Parameters:
a- adoublespecifying the lower limit of integrationb- adoublespecifying the upper limit of integration- Returns:
- a
doublewhich specifies the B-spline integral value fromatob
-
value
public double value(double x)
Returns the value of the B-spline at a point.- Parameters:
x- adoublespecifying the point at which the B-spline is to be evaluated- Returns:
- a
doublegiving the value of the B-spline at the point x
-
value
public double[] value(double[] x)
Returns the value of the B-spline at each point of an array.- Parameters:
x- adoublearray of points at which the B-spline is to be evaluated- Returns:
- a
doublearray containing the value of the B-spline at each point of the arrayx
-
-