- java.lang.Object
-
- com.imsl.math.Bessel
-
-
Method Summary
Methods Modifier and Type Method and Description static double[]I(double xnu, double x, int n)Evaluates a sequence of modified Bessel functions of the first kind with real order and real argument.static double[]I(double x, int n)Evaluates a sequence of modified Bessel functions of the first kind with integer order and real argument.static double[]J(double xnu, double x, int n)Evaluate a sequence of Bessel functions of the first kind with real order and real positive argument.static double[]J(double x, int n)Evaluates a sequence of Bessel functions of the first kind with integer order and real argument.static double[]K(double xnu, double x, int n)Evaluates a sequence of modified Bessel functions of the third kind with fractional order and real argument.static double[]K(double x, int n)Evaluates a sequence of modified Bessel functions of the third kind with integer order and real argument.static double[]scaledK(double v, double x, int n)Evaluate a sequence of exponentially scaled modified Bessel functions of the third kind with fractional order and real argument.static double[]Y(double xnu, double x, int n)Evaluate a sequence of Bessel functions of the second kind with real nonnegative order and real positive argument.
-
-
-
Method Detail
-
I
public static double[] I(double xnu, double x, int n)Evaluates a sequence of modified Bessel functions of the first kind with real order and real argument. The Bessel function , is defined to be
, is defined to be
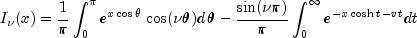
Here, argument
xnuis represented by in the above equation.
in the above equation.The input x must be nonnegative and less than or equal to log(b) (b is the largest representable number). The argument
 =
= xnumust satisfy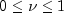 .
.This function is based on a code due to Cody (1983), which uses backward recursion.
- Parameters:
xnu- adoublerepresenting the lowest order desired.xnumust be at least zero and less than 1x- adoublerepresenting the argument of the Bessel functions to be evaluatedn- is theintorder of the last element in the sequence- Returns:
- a
doublearray of lengthn+1containing the values of the function through the series.Bessel.I[i]contains the value of the Bessel function of orderi+xnu.
-
I
public static double[] I(double x, int n)Evaluates a sequence of modified Bessel functions of the first kind with integer order and real argument. The Bessel function is defined to be
is defined to be
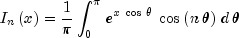
The input
xmust satisfy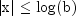 where b is the largest representable floating-point
number. The algorithm is based on a code due to Sookne (1973b), which
uses backward recursion.
where b is the largest representable floating-point
number. The algorithm is based on a code due to Sookne (1973b), which
uses backward recursion.- Parameters:
x- adoublerepresenting the argument of the Bessel functions to be evaluatedn- is theintorder of the last element in the sequence- Returns:
- a
doublearray of lengthn+1containing the values of the function through the series.Bessel.I[i]contains the value of the Bessel function of order i.
-
J
public static double[] J(double xnu, double x, int n)Evaluate a sequence of Bessel functions of the first kind with real order and real positive argument. The Bessel function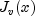 , is defined to be
, is defined to be
This code is based on the work of Gautschi (1964) and Skovgaard (1975). It uses backward recursion.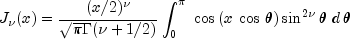
- Parameters:
xnu- adoublerepresenting the lowest order desired.xnumust be at least zero and less than 1.x- adoublerepresenting the argument for which the sequence of Bessel functions is to be evaluatedn- anintrepresenting the order of the last element in the sequence. If order is the highest order desired, setntoint(order).- Returns:
- a
doublearray of lengthn+1containing the values of the function through the series.Bessel.J[I]contains the value of the Bessel function of order I+v atxfor I=0 ton.
-
J
public static double[] J(double x, int n)Evaluates a sequence of Bessel functions of the first kind with integer order and real argument. The Bessel function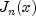 , is defined to be
, is defined to be
The algorithm is based on a code due to Sookne (1973b) that uses backward recursion with strict error control.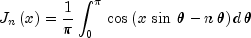
- Parameters:
x- adoublerepresenting the argument for which the sequence of Bessel functions is to be evaluatedn- anintwhich specifies the order of the last element in the sequence- Returns:
- a
doublearray of lengthn+1containing the values of the function through the series.Bessel.J[i]contains the value of the Bessel function of order i atxfor i=0 ton.
-
K
public static double[] K(double xnu, double x, int n)Evaluates a sequence of modified Bessel functions of the third kind with fractional order and real argument. The Bessel function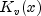 is defined to be
is defined to be
Currently,![K_nu (x) = frac{pi}{2}e^{nu pi i/2} left[
{i,J_nu (ix) - Y_nu (ix)} right] ,,,, rm{for} - pi lt arg ,x
le frac{pi}{2}](eqn_1977.png)
xnu(represented by in
the above equation) is restricted to be less than one in absolute value.
A total of n values is stored in the result,
in
the above equation) is restricted to be less than one in absolute value.
A total of n values is stored in the result, K.K![left[ {rm{0}} right] = K_v (x)](eqn_1979.png) ,
,
K![left[ {rm{1}} right] = K_{v + 1} (x)](eqn_1980.png) ,
,  ,
, K![left[ {n - 1} right] = K_{v + n - 1} (x)](eqn_1982.png) .
.
This method is based on the work of Cody (1983).
- Parameters:
xnu- adoublerepresenting the fractional order of the function.xnumust be less than one in absolute value.x- adoublerepresenting the argument for which the sequence of Bessel functions is to be evaluated.n- anintrepresenting the order of the last element in the sequence. If order is the highest order desired, setnto int(order).- Returns:
- a
doublearray of length n+1 containing the values of the function through the series. Bessel.K[I] contains the value of the Bessel function of order I+v atxfor I=0 ton.
-
K
public static double[] K(double x, int n)Evaluates a sequence of modified Bessel functions of the third kind with integer order and real argument. This function uses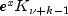 for
for 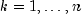 and
and
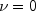 . For the definition of
. For the definition of 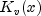 , see above.
, see above.- Parameters:
x- adoublerepresenting the argument for which the sequence of Bessel functions is to be evaluatedn- anintwhich specifies the order of the last element in the sequence- Returns:
- a
doublearray of length n+1 containing the values of the function through the series
-
scaledK
public static double[] scaledK(double v, double x, int n)Evaluate a sequence of exponentially scaled modified Bessel functions of the third kind with fractional order and real argument. This function evaluates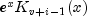 , for i=1,...,n where K
is the modified Bessel function of the third kind. Currently, v is
restricted to be less than 1 in absolute value. A total of
, for i=1,...,n where K
is the modified Bessel function of the third kind. Currently, v is
restricted to be less than 1 in absolute value. A total of
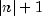 elements are returned in the array. This code
is particularly useful for calculating sequences for large x provided n =
x. (Overflow becomes a problem if
elements are returned in the array. This code
is particularly useful for calculating sequences for large x provided n =
x. (Overflow becomes a problem if 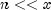 .) n
must not be zero, and x must be greater than zero.
.) n
must not be zero, and x must be greater than zero.  must be less than 1. Also, when
must be less than 1. Also, when  is
large compared with x,
is
large compared with x, 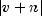 must not be so large
that
must not be so large
that
overflows. The code is based on work of Cody (1983).
- Parameters:
v- adoublerepresenting the fractional order of the function.vmust be less than one in absolute value.x- adoublerepresenting the argument for which the sequence of Bessel functions is to be evaluated.n- anintrepresenting the order of the last element in the sequence. If order is the highest order desired, setnto int(order).- Returns:
- a
doublearray of lengthn+1containing the values of the function through the series. Ifnis positive,Bessel.K[I]contains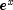 times the value of the Bessel function of order
times the value of the Bessel function of order
I+vatxfor I=0 ton. Ifnis negative,Bessel.K[I]contains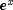 times the value of the Bessel function of order
times the value of the Bessel function of order
v-Iatxfor I=0 ton.
-
Y
public static double[] Y(double xnu, double x, int n)Evaluate a sequence of Bessel functions of the second kind with real nonnegative order and real positive argument. The Bessel function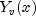 is defined to be
is defined to be
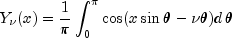
![, - frac{1}{pi }int_0^infty {,left[
{e^{nu t} + e^{ - nu t} ,cos left( {nu pi } right)} right]}
,e^{ - x,sinh ,t} ,dt](eqn_2006.png)
The variable
xnu(represented by in the above equation) must satisfy
in the above equation) must satisfy  . If this condition is not met, then
. If this condition is not met, then Yis set toNaN. In addition,xmust be in![left[ {x_m ,x_M } right]](eqn_2009.png) where
where 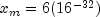 and
and 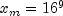 . If
. If 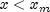 , then the largest representable number is returned; and if
, then the largest representable number is returned; and if
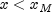 , then zero is returned.
, then zero is returned.The algorithm is based on work of Cody and others, (see Cody et al. 1976; Cody 1969; NATS FUNPACK 1976). It uses a special series expansion for small arguments. For moderate arguments, an analytic continuation in the argument based on Taylor series with special rational minimax approximations providing starting values is employed. An asymptotic expansion is used for large arguments.
- Parameters:
xnu- adoublerepresenting the lowest order desired.xnumust be at least zero and less than 1x- adoublerepresenting the argument for which the sequence of Bessel functions is to be evaluatedn- anintsuch thatn+1elements will be evaluated in the sequence- Returns:
- a
doublearray of lengthn+1containing the values of the function through the series.Bessel.K[I]contains the value of the Bessel function of order I+v atxfor I=0 ton.
-
-