- java.lang.Object
-
- com.imsl.math.BoundedLeastSquares
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class BoundedLeastSquares extends Object implements Serializable, Cloneable
Solves a nonlinear least-squares problem subject to bounds on the variables using a modified Levenberg-Marquardt algorithm.Class
BoundedLeastSquaresuses a modified Levenberg-Marquardt method and an active set strategy to solve nonlinear least-squares problems subject to simple bounds on the variables. The problem is stated as follows: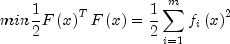
subject to
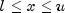
where
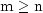 ,
, 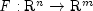 , and
, and 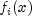 is the
i-th component function of F(x). From a given starting point,
an active set
is the
i-th component function of F(x). From a given starting point,
an active set
IA, which contains the indices of the variables at their bounds, is built. A variable is called a "free variable" if it is not in the active set. The routine then computes the search direction for the free variables according to the formula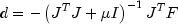
where
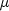 is the Levenberg-Marquardt parameter, F
= F(x), and J is the Jacobian with respect to the free variables.
The search direction for the variables in
is the Levenberg-Marquardt parameter, F
= F(x), and J is the Jacobian with respect to the free variables.
The search direction for the variables in
IAis set to zero. The trust region approach discussed by Dennis and Schnabel (1983) is used to find the new point. Finally, the optimality conditions are checked. The conditions are: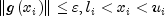
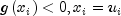
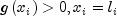
where
 is a gradient tolerance. This
process is repeated until the optimality criterion is achieved.
is a gradient tolerance. This
process is repeated until the optimality criterion is achieved.The active set is changed only when a free variable hits its bounds during an iteration or the optimality condition is met for the free variables but not for all variables in
IA, the active set. In the latter case, a variable that violates the optimality condition will be dropped out ofIA. For more details on the Levenberg-Marquardt method, see Levenberg (1944) or Marquardt (1963). For more detail on the active set strategy, see Gill and Murray (1976).- See Also:
- Example 1, Example 2, Serialized Form
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classBoundedLeastSquares.FalseConvergenceExceptionFalse convergence - The iterates appear to be converging to a noncritical point.static interfaceBoundedLeastSquares.FunctionPublic interface for the user-supplied function to evaluate the function that defines the least-squares problem.static interfaceBoundedLeastSquares.JacobianPublic interface for the user-supplied function to compute the Jacobian.
-
Constructor Summary
Constructors Constructor and Description BoundedLeastSquares(BoundedLeastSquares.Function function, int mFunctions, int nVariables, int boundType, double[] lowerBound, double[] upperBound)Constructor forBoundedLeastSquares.
-
Method Summary
Methods Modifier and Type Method and Description double[][]getJacobian()Returns the Jacobian at the approximate solution.intgetNumberOfThreads()Returns the number ofjava.lang.Threadinstances used for parallel processing.double[]getResiduals()Returns the residuals at the approximate solution.double[]getSolution()Returns the solution.voidsetAbsoluteFcnTol(double absoluteFcnTol)Sets the absolute function tolerance.voidsetDiagonalScalingMatrix(double[] diagonalScalingMatrix)Sets the diagonal scaling matrix for the functions.voidsetGoodDigit(int goodDigit)Sets the number of good digits in the function.voidsetGradientTol(double gradientTol)Sets the scaled gradient tolerance.voidsetGuess(double[] guess)Sets the initial guess of the solution.voidsetInternalScale()Sets the internal variable scaling option.voidsetJacobian(BoundedLeastSquares.Jacobian jacobian)Sets the Jacobian.voidsetMaximumFunctionEvals(int evaluations)Sets the maximum number of function evaluations.voidsetMaximumIteration(int iterations)Sets the maximum number of iterations.voidsetMaximumJacobianEvals(int evaluations)Sets the maximum number of Jacobian evaluations.voidsetMaximumStepSize(double stepSize)Sets the maximum allowable step size.voidsetNumberOfThreads(int numberOfThreads)Sets the number ofjava.lang.Threadinstances to be used for parallel processing.voidsetRelativeFcnTol(double relativeFcnTol)Sets the relative function tolerance.voidsetScaledStepTol(double scaledStepTol)Sets the scaled step tolerance.voidsetScalingVector(double[] scalingVector)Sets the scaling vector for the variables.voidsetTrustRegion(double trustRegion)Sets the size of initial trust region radius.voidsolve()Solves a nonlinear least-squares problem subject to bounds on the variables using a modified Levenberg-Marquardt algorithm.
-
-
-
Constructor Detail
-
BoundedLeastSquares
public BoundedLeastSquares(BoundedLeastSquares.Function function, int mFunctions, int nVariables, int boundType, double[] lowerBound, double[] upperBound)
Constructor forBoundedLeastSquares.- Parameters:
function- aFunctionobject, user-supplied function to evaluate the functionmFunctions- anintscalar containing the number of functionsnVariables- anintscalar containing the number of variablesboundType- anintscalar containing the types of bounds on the variableboundType Action 0 User will supply all the bounds. 1 All variables are nonnegative. 2 All variables are nonpositive. 3 User supplies only the bounds on first variable, all other variables will have the same bounds. lowerBound- adoublearray containing the lower bounds on the variablesupperBound- adoublearray containing the upper bounds on the variables- Throws:
IllegalArgumentException- is thrown if the dimensions ofmFunctions,nVariables,boundType,lowerBound.lengthandupperBound.lengthare not consistent
-
-
Method Detail
-
getJacobian
public double[][] getJacobian()
Returns the Jacobian at the approximate solution.- Returns:
- a
mFunctions x nVariables doublematrix containing the Jacobian at the approximate solution
-
getNumberOfThreads
public int getNumberOfThreads()
Returns the number ofjava.lang.Threadinstances used for parallel processing.- Returns:
- an
intcontaining the number ofjava.lang.Threadinstances used for parallel processing.
-
getResiduals
public double[] getResiduals()
Returns the residuals at the approximate solution.- Returns:
- a
doublearray containing the residuals at the approximate solution
-
getSolution
public double[] getSolution()
Returns the solution.- Returns:
- a
doublearray containing the computed solution
-
setAbsoluteFcnTol
public void setAbsoluteFcnTol(double absoluteFcnTol)
Sets the absolute function tolerance. If this member function is not called, a value of Math.max(1.0e-10, Math.pow(2.2204460492503131e-16, 2.0/3.0)), is used.- Parameters:
absoluteFcnTol- adoublescalar containing the absolute function tolerance
-
setDiagonalScalingMatrix
public void setDiagonalScalingMatrix(double[] diagonalScalingMatrix)
Sets the diagonal scaling matrix for the functions. The i-th component of the array is a positive scalar specifying the reciprocal magnitude of the i-th component function of the problem. If this member function is not called, an initial scaling of 1.0 is used.- Parameters:
diagonalScalingMatrix- adoublearray containing the diagonal scaling for the functions
-
setGoodDigit
public void setGoodDigit(int goodDigit)
Sets the number of good digits in the function. If this member function is not called, a value of (int)(-Sfun.log10(2.2204460492503131e-16) + 0.1e0) is used.- Parameters:
goodDigit- anintscalar containing the number of good digits
-
setGradientTol
public void setGradientTol(double gradientTol)
Sets the scaled gradient tolerance. If this member function is not called, a value of Math.pow(2.2204460492503131e-16, 1.0e0/3.0e0) is used.- Parameters:
gradientTol- adoublescalar containing the scaled gradient tolerance
-
setGuess
public void setGuess(double[] guess)
Sets the initial guess of the solution. If this member function is not called, an initial scaling of 1.0 is used.- Parameters:
guess- adoublearray containing an initial guess
-
setInternalScale
public void setInternalScale()
Sets the internal variable scaling option. With this option, scaling for the variables is set internally.
-
setJacobian
public void setJacobian(BoundedLeastSquares.Jacobian jacobian)
Sets the Jacobian.- Parameters:
jacobian- aJacobianobject to compute the Jacobian.
-
setMaximumFunctionEvals
public void setMaximumFunctionEvals(int evaluations)
Sets the maximum number of function evaluations. If this member function is not called, a value of 400 is used.- Parameters:
evaluations- anintscalar containing the maximum number of function evaluations
-
setMaximumIteration
public void setMaximumIteration(int iterations)
Sets the maximum number of iterations. If this member function is not called, a value of 100 is used.- Parameters:
iterations- anintscalar containing the maximum number of iterations
-
setMaximumJacobianEvals
public void setMaximumJacobianEvals(int evaluations)
Sets the maximum number of Jacobian evaluations. If this member function is not called, a value of 400 is used.- Parameters:
evaluations- anintscalar containing the maximum number of Jacobian evaluations
-
setMaximumStepSize
public void setMaximumStepSize(double stepSize)
Sets the maximum allowable step size.- Parameters:
stepSize- adoublescalar containing the maximum allowable step size
-
setNumberOfThreads
public void setNumberOfThreads(int numberOfThreads)
Sets the number ofjava.lang.Threadinstances to be used for parallel processing.- Parameters:
numberOfThreads- anintspecifying the number ofjava.lang.Threadinstances to be used for parallel processing. IfnumberOfThreadsis greater than 1, then interfaceFunction.computeis evaluated in parallel andFunction.computemust be thread-safe. Otherwise, unexpected behavior can occur.Default:
numberOfThreads= 1.
-
setRelativeFcnTol
public void setRelativeFcnTol(double relativeFcnTol)
Sets the relative function tolerance. If this member function is not called, a value of Math.pow(2.2204460492503131e-16, 2.0e0/3.0e0) is used.- Parameters:
relativeFcnTol- adoublescalar containing the relative function tolerance
-
setScaledStepTol
public void setScaledStepTol(double scaledStepTol)
Sets the scaled step tolerance. If this member function is not called, a value of Math.max(1.0e-10, Math.pow(2.2204460492503131e-16, 2.0e0/3.0e0) is used.- Parameters:
scaledStepTol- adoublescalar containing the scaled step tolerance
-
setScalingVector
public void setScalingVector(double[] scalingVector)
Sets the scaling vector for the variables. If this member function is not called, an initial scaling of 1.0 is used.- Parameters:
scalingVector- adoublearray containing the scaling vector for the variables
-
setTrustRegion
public void setTrustRegion(double trustRegion)
Sets the size of initial trust region radius. If this member function is not called, the value is based on the initial scaled Cauchy step.- Parameters:
trustRegion- adoublescalar containing the initial trust region radius
-
solve
public final void solve() throws BoundedLeastSquares.FalseConvergenceExceptionSolves a nonlinear least-squares problem subject to bounds on the variables using a modified Levenberg-Marquardt algorithm.- Throws:
BoundedLeastSquares.FalseConvergenceException- is thrown when the iterates appear to be converging to a noncritical point.
-
-