- java.lang.Object
-
- com.imsl.math.ComplexFFT
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class ComplexFFT extends Object implements Serializable, Cloneable
Complex FFT.Class
ComplexFFTcomputes the discrete complex Fourier transform of a complex vector of size N. The method used is a variant of the Cooley-Tukey algorithm, which is most efficient when N is a product of small prime factors. If N satisfies this condition, then the computational effort is proportional to N log N. This considerable savings has historically led people to refer to this algorithm as the "fast Fourier transform" or FFT.Specifically, given an N-vector
 ,
method
,
method forwardreturns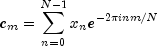
Furthermore, a vector of Euclidean norm S is mapped into a vector of norm
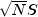
Finally, note that we can invert the Fourier transform as follows:
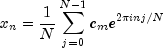
This formula reveals the fact that, after properly normalizing the Fourier coefficients, one has the coefficients for a trigonometric interpolating polynomial to the data. An unnormalized inverse is implemented in
backward.ComplexFFTis based on the complex FFT in FFTPACK. The package, FFTPACK was developed by Paul Swarztrauber at the National Center for Atmospheric Research.Specifically, given an N-vector c,
backwardreturns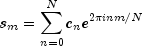
Furthermore, a vector of Euclidean norm S is mapped into a vector of norm
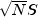
Finally, note that we can invert the inverse Fourier transform as follows:
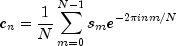
This formula reveals the fact that, after properly normalizing the Fourier coefficients, one has the coefficients for a trigonometric interpolating polynomial to the data. backward is based on the complex inverse FFT in FFTPACK. The package, FFTPACK was developed by Paul Swarztrauber at the National Center for Atmospheric Research.
- See Also:
- Example, Serialized Form
-
-
Constructor Summary
Constructors Constructor and Description ComplexFFT(int n)Constructs a complex FFT object.
-
-
-
Constructor Detail
-
ComplexFFT
public ComplexFFT(int n)
Constructs a complex FFT object.- Parameters:
n- is the array size that this object can handle.
-
-