-
- Enclosing class:
- FeynmanKac
public static interface FeynmanKac.PdeCoefficientsPublic interface for user supplied PDE coefficients in the Feynman-Kac PDE.
-
-
Method Summary
Methods Modifier and Type Method and Description doublekappa(double x, double t)Returns the value of the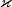 coefficient at the given point.
coefficient at the given point.doublemu(double x, double t)Returns the value of the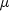 coefficient at the given point.
coefficient at the given point.doublesigma(double x, double t)Returns the value of the coefficient at the given point.
coefficient at the given point.doublesigmaPrime(double x, double t)Returns the value of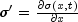 at the given point.
at the given point.
-
-
-
Method Detail
-
kappa
double kappa(double x, double t)Returns the value of the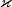 coefficient at the given point.
coefficient at the given point.
Time dependency of
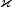 can be controlled via method
can be controlled via method
setTimeDependence. Use of this method will usually yield a more efficient algorithm because some finite element matrices do not have to be reassembled for eachtvalue.- Parameters:
x- adouble, the point in space at which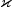 is to be evaluated.
is to be evaluated.t- adouble, the time point at which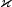 is
to be evaluated.
is
to be evaluated.- Returns:
- a
double, the value of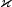 at
at (x,t).
-
mu
double mu(double x, double t)Returns the value of the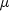 coefficient at the given point.
coefficient at the given point.
Time dependency of
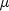 can be controlled via method
can be controlled via method
setTimeDependence. Use of this method will usually yield a more efficient algorithm because some finite element matrices do not have to be reassembled for eachtvalue.- Parameters:
x- adouble, the point in space at which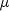 is to be evaluated.
is to be evaluated.t- adouble, the time point at which is
to be evaluated.
is
to be evaluated.- Returns:
- a
double, the value of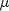 at
at (x,t).
-
sigma
double sigma(double x, double t)Returns the value of the coefficient at the given point.
coefficient at the given point.
Time dependency of
 can be controlled via method
can be controlled via method
setTimeDependence. Use of this method will usually yield a more efficient algorithm because some finite element matrices do not have to be reassembled for eachtvalue.- Parameters:
x- adouble, the point in space at which is to be evaluated.
is to be evaluated.t- adouble, the time point at which is
to be evaluated.
is
to be evaluated.- Returns:
- a
double, the value of at
at (x,t).
-
sigmaPrime
double sigmaPrime(double x, double t)Returns the value of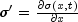 at the given point.
at the given point.
Time dependency of
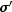 can be controlled via method
can be controlled via method
setTimeDependence. Use of this method will usually yield a more efficient algorithm because some finite element matrices do not have to be reassembled for eachtvalue.- Parameters:
x- adouble, the point in space at which is to be evaluated.
is to be evaluated.t- adouble, the time point at which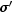 is to be evaluated.
is to be evaluated.- Returns:
- a
double, the value of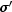 at
at
(x,t).
-
-