- java.lang.Object
-
- com.imsl.math.MinConNLP
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class MinConNLP extends Object implements Serializable, Cloneable
General nonlinear programming solver.MinConNLPis based on the FORTRAN subroutine,DONLP2, by Peter Spellucci and licensed from TU Darmstadt.MinConNLPuses a sequential equality constrained quadratic programming method with an active set technique, and an alternative usage of a fully regularized mixed constrained subproblem in case of nonregular constraints (i.e. linear dependent gradients in the "working sets"). It uses a slightly modified version of the Pantoja-Mayne update for the Hessian of the Lagrangian, variable dual scaling and an improved Armjijo-type stepsize algorithm. Bounds on the variables are treated in a gradient-projection like fashion. Details may be found in the following two papers:P. Spellucci: An SQP method for general nonlinear programs using only equality constrained subproblems. Math. Prog. 82, (1998), 413-448.
P. Spellucci: A new technique for inconsistent problems in the SQP method. Math. Meth. of Oper. Res. 47, (1998), 355-500. (published by Physica Verlag, Heidelberg, Germany).
The problem is stated as follows:
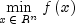
subject to
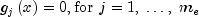
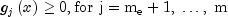
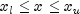
where all problem functions are assumed to be continuously differentiable. Although default values are provided for optional input arguments, it may be necessary to adjust these values for some problems. Through the use of member functions,
MinConNLPallows for several parameters of the algorithm to be adjusted to account for specific characteristics of problems. TheDONLP2Users Guide provides detailed descriptions of these parameters as well as strategies for maximizing the performance of the algorithm. In addition, the following are a number of guidelines to consider when usingMinConNLP:- A good initial starting point is very problem specific and should be provided
by the calling program whenever possible. See method
setGuess. - Gradient approximation methods can have an effect on the success of
MinConNLP. Selecting a higher order approximation method may be necessary for some problems. See methodsetDifferentiationType. - If a two sided constraint
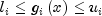 is transformed
into two constraints,
is transformed
into two constraints, 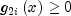 and
and 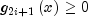 ,
then choose
,
then choose 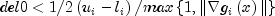 , or at least
try to provide an estimate for that value. This will increase the efficiency of the algorithm. See method
, or at least
try to provide an estimate for that value. This will increase the efficiency of the algorithm. See method setBindingThreshold. - The parameter
ierrprovided in the interface to the user supplied functionFCNcan be very useful in cases when evaluation is requested at a point that is not possible or reasonable. For example, if evaluation at the requested point would result in a floating point exception, then settingierrtotrueand returning without performing the evaluation will avoid the exception.MinConNLPwill then reduce the stepsize and try the step again. Note, ifierris set totruefor the initial guess, then an error is issued.
The solver terminates if there is an error or if one of the following three terminations conditions is satisfied. The method
getTerminationConditionreturns the termination condition index.- Termination condition 10: Kuhn-Tucker conditions are satisfied.
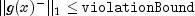

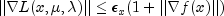
where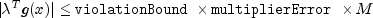
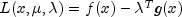 ,
M is the number of constraints, and
,
M is the number of constraints, and
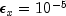 .
The notation
.
The notation 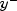 means a vector
whose negative elements are the same as the vector y,
but with zeros in place of y's positive values.
means a vector
whose negative elements are the same as the vector y,
but with zeros in place of y's positive values.
- Termination condition 11: Computed correction is small.
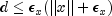
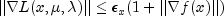
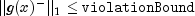
where d is the computed correction for the current solution x.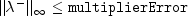
- Termination condition 12: x is almost feasible, directional derivative is very small.
Further progress cannot be expected.
where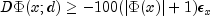
 is the current penalty function, and
is the current penalty function, and
 is the directional derivative of
is the directional derivative of 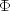 .
This usually occurs as a termination condition for ill-conditioned problems.
.
This usually occurs as a termination condition for ill-conditioned problems.
Note that one can use the JDK 1.4 JAVA Logging API to generate intermediate output for the solver. Accumulated levels of detail correspond to JAVA's CONFIG, FINE, FINER, and FINEST logging levels with CONFIG yielding the smallest amount of information and FINEST yielding the most. The levels of output yield the following:
Level Output CONFIG One line of intermediate results is printed with each iteration. A summary report is printed upon completion. FINE Lines of intermediate results giving the most important data for each step are printed after each step. A summary report is printed upon completion. FINER Lines of detailed intermediate results showing all primal and dual variables, the relevant values from the working set, progress in the backtracking, etc. are printed. A summary report is printed upon completion. FINEST Lines of detailed intermediate results showing all primal and dual variables, the relevant values from the working set, progress in the backtracking, the gradients in the working set, the quasi-Newton updated, etc. are printed. A summary report is printed upon completion.
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classMinConNLP.BadInitialGuessExceptionPenalty function point infeasible for original problem.static classMinConNLP.ConstraintEvaluationExceptionConstraint evaluation returns an error with current point.static interfaceMinConNLP.FunctionPublic interface for the user supplied function to theMinConNLPobject.static interfaceMinConNLP.GradientPublic interface for the user supplied function to compute the gradient forMinConNLPobject.static classMinConNLP.IllConditionedExceptionProblem is singular or ill-conditioned.static classMinConNLP.LimitingAccuracyExceptionLimiting accuracy reached for a singular problem.static classMinConNLP.LinearlyDependentGradientsExceptionWorking set gradients are linearly dependent.static classMinConNLP.NoAcceptableStepsizeExceptionNo acceptable stepsize in [SIGMA,SIGLA].static classMinConNLP.ObjectiveEvaluationExceptionObjective evaluation returns an error with current point.static classMinConNLP.PenaltyFunctionPointInfeasibleExceptionPenalty function point infeasible.static classMinConNLP.QPInfeasibleExceptionQP problem seemingly infeasible.static classMinConNLP.SingularExceptionProblem is singular.static classMinConNLP.TerminationCriteriaNotSatisfiedExceptionTermination criteria are not satisfied.static classMinConNLP.TooManyIterationsExceptionMaximum number of iterations exceeded.static classMinConNLP.TooMuchTimeExceptionMaximum time allowed for solve exceeded.static classMinConNLP.WorkingSetSingularExceptionWorking set is singular in dual extended QP.
-
Constructor Summary
Constructors Constructor and Description MinConNLP(int mTotalConstraints, int mEqualityConstraints, int nVariables)Nonlinear programming solver constructor.
-
Method Summary
Methods Modifier and Type Method and Description double[]getConstraintResiduals()Returns the constraint residuals.intgetIterations()Returns the actual number of iterations used.double[]getLagrangeMultiplierEst()Returns the Lagrange multiplier estimates of the constraints.LoggergetLogger()Returns the logger object.longgetMaximumTime()Returns the maximum time allowed for the solve step.intgetNumberOfThreads()Returns the number ofjava.lang.Threadinstances used for parallel processing.doublegetOptimalValue()Returns the value of the objective function.double[]getSolution()Returns the last computed solution.intgetTerminationCriterion()Returns the reason the solve step terminated.doublegetTolerance()Returns the desired precision of the solution.voidsetBindingThreshold(double del0)Set the binding threshold for constraints.voidsetBoundViolationBound(double taubnd)Set the amount by which bounds may be violated during numerical differentiation.voidsetDifferentiationType(int idtype)Set the type of numerical differentiation to be used.voidsetFunctionPrecision(double epsfcn)Set the relative precision of the function evaluation routine.voidsetGradientPrecision(double epsdif)Set the relative precision in gradients.voidsetGuess(double[] xguess)Set the initial guess of the minimum point of the input function.voidsetMaximumTime(long maximumTime)Sets the maximum time allowed for the solve step.voidsetMaxIterations(int maxIterations)Set the maximum number of iterations allowed.voidsetMultiplierError(double smallw)Set the error allowed in the multipliers.voidsetNumberOfThreads(int numberOfThreads)Sets the number ofjava.lang.Threadinstances to be used for parallel processing.voidsetPenaltyBound(double tau0)Set the universal bound for describing how much the unscaled penalty-term may deviate from zero.voidsetScalingBound(double scbnd)Set the scaling bound for the internal automatic scaling of the objective function.voidsetTolerance(double epsx)Set the desired precision of the solution.voidsetViolationBound(double delmin)Set the scalar which defines allowable constraint violations of the final accepted result.voidsetXlowerBound(double[] xlb)Set the lower bounds on the variables.voidsetXscale(double[] xscale)Set the internal scaling of the variables.voidsetXupperBound(double[] xub)Set the upper bounds on the variables.double[]solve(MinConNLP.Function F)Solve a general nonlinear programming problem using the successive quadratic programming algorithm with a finite-difference gradient or with a user-supplied gradient.
-
-
-
Constructor Detail
-
MinConNLP
public MinConNLP(int mTotalConstraints, int mEqualityConstraints, int nVariables) throws IllegalArgumentExceptionNonlinear programming solver constructor.- Parameters:
mTotalConstraints- Anintscalar value which defines the total number of constraintsmEqualityConstraints- Anintscalar value which defines the number of equality constraintsnVariables- Anintscalar value which defines the number of variables.- Throws:
IllegalArgumentException
-
-
Method Detail
-
getConstraintResiduals
public double[] getConstraintResiduals()
Returns the constraint residuals.- Returns:
- a
doublearray containing the constraint residuals.
-
getIterations
public int getIterations()
Returns the actual number of iterations used.- Returns:
- the number of iterations used.
-
getLagrangeMultiplierEst
public double[] getLagrangeMultiplierEst()
Returns the Lagrange multiplier estimates of the constraints.- Returns:
- a
doublearray containing the Lagrange multiplier estimates of the constraints.
-
getLogger
public Logger getLogger()
Returns the logger object. Logger support requires JDK1.4. Use with earlier versions returns null.- Returns:
- the logger object, if present, or null.
-
getMaximumTime
public long getMaximumTime()
Returns the maximum time allowed for the solve step.- Returns:
- the maximum time, in milliseconds, to be allowed for the solve step. If less than or equal to zero then no time limit is imposed. The default valus is -1 (no time limit).
-
getNumberOfThreads
public int getNumberOfThreads()
Returns the number ofjava.lang.Threadinstances used for parallel processing.- Returns:
- an
intcontaining the number ofjava.lang.Threadinstances used for parallel processing.
-
getOptimalValue
public double getOptimalValue()
Returns the value of the objective function.- Returns:
- a
double, the value of the objective function.
-
getSolution
public double[] getSolution()
Returns the last computed solution. This is the same solution as returned by thesolvemethod.- Returns:
- a
doublearray containing the solution.
-
getTerminationCriterion
public int getTerminationCriterion()
Returns the reason the solve step terminated.- Returns:
- an
intthat indicates the reason the solve method terminated. - See Also:
- List of termination condtions
-
getTolerance
public double getTolerance()
Returns the desired precision of the solution.- Returns:
- a
doublethat is the the desired precision of the solution.
-
setBindingThreshold
public void setBindingThreshold(double del0)
Set the binding threshold for constraints. In the initial phase of minimization a constraint is considered binding if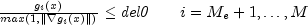
Good values are between .01 and 1.0. If del0 is chosen too small then identification of the correct set of binding constraints may be delayed. Contrary, if del0 is too large, then the method will often escape to the full regularized SQP method, using individual slack variables for any active constraint, which is quite costly. For well scaled problems del0 = 1.0 is reasonable. If this member function is not called, del0 is set to .5 * tau0.
- Parameters:
del0- adoublescalar value specifying the binding threshold for constraints.- Throws:
IllegalArgumentException- is thrown if del0 is less than or equal to 0.0
-
setBoundViolationBound
public void setBoundViolationBound(double taubnd)
Set the amount by which bounds may be violated during numerical differentiation. If this member function is not called, taubnd is set to 1.0.- Parameters:
taubnd- adoublescalar value specifying the amount by which bounds may be violated during numerical differentiation.- Throws:
IllegalArgumentException- is thrown if taubnd is less than or equal to 0.0
-
setDifferentiationType
public void setDifferentiationType(int idtype)
Set the type of numerical differentiation to be used.- Parameters:
idtype- anintscalar value specifying the type of numerical differentiation to be used. If this member function is not called, idtype is set to 1.idtype Action 1 Use a forward difference quotient with discretization stepsize  componentwise relative. This is the default value used.
componentwise relative. This is the default value used. 2 Use the symmetric difference quotient with discretization stepsize 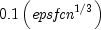 componentwise relative.
componentwise relative. 3 Use the sixth order approximation computing a Richardson extrapolation of three symmetric difference quotient values. This uses a discretization stepsize 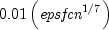
- Throws:
IllegalArgumentException- is thrown if idtype is less than or equal to 0 or greater than or equal to 4.
-
setFunctionPrecision
public void setFunctionPrecision(double epsfcn)
Set the relative precision of the function evaluation routine. If this member function is not called, epsfcn is set to 2.2e-16.- Parameters:
epsfcn- adoublescalar value specifying the relative precision of the function evaluation routine.- Throws:
IllegalArgumentException- is thrown if epsfcn is less than or equal to 0.0
-
setGradientPrecision
public void setGradientPrecision(double epsdif)
Set the relative precision in gradients. If this member function is not called, epsdif is set to 2.2e-16.- Parameters:
epsdif- adoublescalar value specifying the relative precision in gradients.- Throws:
IllegalArgumentException- is thrown if epsdif is less than or equal to 0.0
-
setGuess
public void setGuess(double[] xguess)
Set the initial guess of the minimum point of the input function. If this member function is not called, the elements of this array are set to x, (with the smallest value of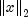 ) that satisfies the bounds.
) that satisfies the bounds.- Parameters:
xguess- adoublearray specifying the initial guess of the minimum point of the input function
-
setMaximumTime
public void setMaximumTime(long maximumTime)
Sets the maximum time allowed for the solve step.- Parameters:
maximumTime- is the maximum time, in milliseconds, to be allowed for the solve step. If less than or equal to zero then no time limit is imposed.
-
setMaxIterations
public void setMaxIterations(int maxIterations)
Set the maximum number of iterations allowed. If this member function is not called, the maximum number of iterations is set to 200.- Parameters:
maxIterations- anintspecifying the maximum number of iterations allowed- Throws:
IllegalArgumentException- is thrown ifmaxIterationsis less than or equal to 0
-
setMultiplierError
public void setMultiplierError(double smallw)
Set the error allowed in the multipliers. A negative multiplier of an inequality constraint is accepted (as zero) if its absolute value is less than smallw. If this member function is not called, it is set to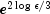 .
.- Parameters:
smallw- adoublescalar value specifying the error allowed in the multipliers.- Throws:
IllegalArgumentException- is thrown if smallw is less than or equal to 0.0
-
setNumberOfThreads
public void setNumberOfThreads(int numberOfThreads)
Sets the number ofjava.lang.Threadinstances to be used for parallel processing.- Parameters:
numberOfThreads- anintspecifying the number ofjava.lang.Threadinstances to be used for parallel processing. IfnumberOfThreadsis greater than 1, then interfaceFunction.fis evaluated in parallel andFunction.fmust be thread-safe. Otherwise, unexpected behavior can occur.Default:
numberOfThreads= 1.
-
setPenaltyBound
public void setPenaltyBound(double tau0)
Set the universal bound for describing how much the unscaled penalty-term may deviate from zero. A small tau0 diminishes the efficiency of the solver because the iterates then will follow the boundary of the feasible set closely. Conversely, a large tau0 may degrade the reliability of the code. If this member function is not called, tau0 is set to 1.0.- Parameters:
tau0- adoublescalar value specifying the universal bound for describing how much the unscaled penalty-term may deviate from zero.- Throws:
IllegalArgumentException- is thrown if tau0 is less than or equal to 0.0
-
setScalingBound
public void setScalingBound(double scbnd)
Set the scaling bound for the internal automatic scaling of the objective function. If this member function is not called, scbnd is set to 1.0e4.- Parameters:
scbnd- adoublescalar value specifying the scaling variable for the problem function.- Throws:
IllegalArgumentException- is thrown if scbnd is less than or equal to 0.0
-
setTolerance
public void setTolerance(double epsx)
Set the desired precision of the solution.- Parameters:
epsx- is the the desired precision of the solution. For a well scaled and well-conditioned problem it essentially specifies a desired relative precision in the solution. It should never be chosen less than the square root of the machine precision since the control of progress in the method is based on the comparison of function values usually taken from the constraining manifold where the objective function varies like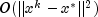 . Even this requirement may be too strong. The
default value of 1.0e-5 is approximately the third root of
the machine precision. The user should be aware of the
fact that the precision requirement is automatically
relaxed if the solver considers a problem "singular". If
the precision seems to be too poor in such a case a
decrease of
. Even this requirement may be too strong. The
default value of 1.0e-5 is approximately the third root of
the machine precision. The user should be aware of the
fact that the precision requirement is automatically
relaxed if the solver considers a problem "singular". If
the precision seems to be too poor in such a case a
decrease of epsxmight help. Default: 1.0e-5.
-
setViolationBound
public void setViolationBound(double delmin)
Set the scalar which defines allowable constraint violations of the final accepted result. Constraints are satisfied if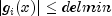 , and
, and
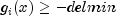 respectively. If this
member function is not called, delmin is set to
respectively. If this
member function is not called, delmin is set to
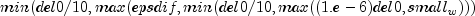 .
.- Parameters:
delmin- adoublescalar value specifying the allowable constraint violations of the final accepted result.- Throws:
IllegalArgumentException- is thrown if delmin is less than or equal to 0.0
-
setXlowerBound
public void setXlowerBound(double[] xlb)
Set the lower bounds on the variables. If this member function is not called, the elements of this array are set to -1.79e308.- Parameters:
xlb- adoublearray specifying the lower bounds on the variables
-
setXscale
public void setXscale(double[] xscale)
Set the internal scaling of the variables. The initial value given and the objective function and gradient evaluations, however, are always given in the original unscaled variables. The first internal variable is obtained by dividing the values x[i] by xscale[i]. If this member function is not called, xscale[i] is set to 1.0.- Parameters:
xscale- adoublearray specifying the internal scaling of the variables.- Throws:
IllegalArgumentException- is thrown if xscale is less than or equal to 0.0
-
setXupperBound
public void setXupperBound(double[] xub)
Set the upper bounds on the variables. If this member function is not called, the elements of this array are set to 1.79e308.- Parameters:
xub- adoublearray specifying the upper bounds on the variables
-
solve
public double[] solve(MinConNLP.Function F) throws MinConNLP.ConstraintEvaluationException, MinConNLP.ObjectiveEvaluationException, MinConNLP.WorkingSetSingularException, MinConNLP.QPInfeasibleException, MinConNLP.PenaltyFunctionPointInfeasibleException, MinConNLP.LimitingAccuracyException, MinConNLP.TooManyIterationsException, MinConNLP.BadInitialGuessException, MinConNLP.IllConditionedException, MinConNLP.SingularException, MinConNLP.LinearlyDependentGradientsException, MinConNLP.NoAcceptableStepsizeException, MinConNLP.TerminationCriteriaNotSatisfiedException
Solve a general nonlinear programming problem using the successive quadratic programming algorithm with a finite-difference gradient or with a user-supplied gradient.- Parameters:
F- defines the user-supplied function to evaluate the function at a given point. F can be used to supply a gradient of the function. If F implementsGradientthe user-supplied gradient is used. Otherwise,an attempt to solve the problem is made using a finite-difference gradient.- Returns:
- a
doublearray containing the solution of the nonlinear programming problem. - Throws:
MinConNLP.ConstraintEvaluationExceptionMinConNLP.ObjectiveEvaluationExceptionMinConNLP.WorkingSetSingularExceptionMinConNLP.QPInfeasibleExceptionMinConNLP.PenaltyFunctionPointInfeasibleExceptionMinConNLP.LimitingAccuracyExceptionMinConNLP.TooManyIterationsExceptionMinConNLP.BadInitialGuessExceptionMinConNLP.IllConditionedExceptionMinConNLP.SingularExceptionMinConNLP.LinearlyDependentGradientsExceptionMinConNLP.NoAcceptableStepsizeExceptionMinConNLP.TerminationCriteriaNotSatisfiedException
-
-