- java.lang.Object
-
- com.imsl.math.QuadraticProgramming
-
public class QuadraticProgramming extends Object
Solves the convex quadratic programming problem subject to equality or inequality constraints.Class
QuadraticProgrammingis based on M.J.D. Powell's implementation of the Goldfarb and Idnani dual quadratic programming (QP) algorithm for convex QP problems subject to general linear equality/inequality constraints (Goldfarb and Idnani 1983); i.e., problems of the form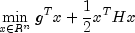
subject to
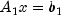
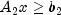
given the vectors
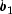 ,
, 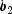 , and
g, and the matrices H,
, and
g, and the matrices H, 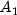 ,
and
,
and 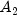 . H is required to be
positive definite. In this case, a unique x solves the
problem or the constraints are inconsistent. If H is not
positive definite, a positive definite perturbation of H
is used in place of H. For more details, see Powell
(1983, 1985).
. H is required to be
positive definite. In this case, a unique x solves the
problem or the constraints are inconsistent. If H is not
positive definite, a positive definite perturbation of H
is used in place of H. For more details, see Powell
(1983, 1985).If a perturbation of H,
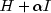 ,
is used in the QP problem, then
,
is used in the QP problem, then
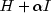 also should be used in the definition of
the Lagrange multipliers.
also should be used in the definition of
the Lagrange multipliers.If the constraints are infeasible an exception is thrown. See Example 3 where the exception is caught and printed.
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classQuadraticProgramming.InconsistentSystemExceptionThe system of constraints is inconsistent.static classQuadraticProgramming.NoLPSolutionExceptionNo solution for the LP problem with h = 0 was found byDenseLP.static classQuadraticProgramming.ProblemUnboundedExceptionThe object value for the problem is unbounded.static classQuadraticProgramming.SolutionNotFoundExceptionA solution was not found.
-
Field Summary
Fields Modifier and Type Field and Description static doubleEPSILON_SMALLThe smallest relative spacing for doubles.
-
Constructor Summary
Constructors Constructor and Description QuadraticProgramming(double[][] h, double[] g, double[][] aEquality, double[] bEquality, double[][] aInequality, double[] bInequality)Solve a quadratic programming problem.
-
Method Summary
Methods Modifier and Type Method and Description double[]getDual()Returns the dual (Lagrange multipliers).doublegetOptimalValue()Returns the optimal value.double[]getSolution()Returns the solution.booleanisNoMoreProgress()Returns true if due to computer rounding error, a change in the variables fail to improve the objective function.
-
-
-
Field Detail
-
EPSILON_SMALL
public static final double EPSILON_SMALL
The smallest relative spacing for doubles.- See Also:
- Constant Field Values
-
-
Constructor Detail
-
QuadraticProgramming
public QuadraticProgramming(double[][] h, double[] g, double[][] aEquality, double[] bEquality, double[][] aInequality, double[] bInequality) throws QuadraticProgramming.InconsistentSystemException, QuadraticProgramming.ProblemUnboundedException, QuadraticProgramming.NoLPSolutionException, QuadraticProgramming.SolutionNotFoundExceptionSolve a quadratic programming problem.- Parameters:
h- is square array containing the Hessian. It must be positive definite.g- contains the coefficients of the linear term of the objective function.aEquality- is a rectangular matrix containing the equality constraints. It can be null if there are no equality constraints.bEquality- contains the right-side of the equality constraints. It can be null if there are no equality constraints.aInequality- is a rectangular matrix containing the inequality constraints. It can be null if there are no inequality constraints.bInequality- contains the right-side of the inequality constraints. It can be null if there are no inequality constraints.- Throws:
QuadraticProgramming.InconsistentSystemException- if the system of constraints is inconsistent and there is no solution.QuadraticProgramming.ProblemUnboundedExceptionQuadraticProgramming.NoLPSolutionExceptionQuadraticProgramming.SolutionNotFoundException
-
-
Method Detail
-
getDual
public double[] getDual()
Returns the dual (Lagrange multipliers).
-
getOptimalValue
public double getOptimalValue()
Returns the optimal value.- Returns:
- a
double, the optimal value.
-
getSolution
public double[] getSolution()
Returns the solution.
-
isNoMoreProgress
public boolean isNoMoreProgress()
Returns true if due to computer rounding error, a change in the variables fail to improve the objective function. Usually the solution is close to optimum.
-
-