Computes approximations to the forcing term
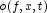
and its derivative
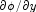
.
(in ImslCS.dll) Version: 6.5.0.0
 Syntax
Syntax
| C# |
|---|
void Force(
int interval,
double[] y,
double time,
double width,
double[] xlocal,
double[] qw,
double[,] u,
double[] phi,
double[,] dphi
) |
| Visual Basic (Declaration) |
|---|
Sub Force ( _
interval As Integer, _
y As Double(), _
time As Double, _
width As Double, _
xlocal As Double(), _
qw As Double(), _
u As Double(,), _
phi As Double(), _
dphi As Double(,) _
) |
| Visual C++ |
|---|
void Force(
int interval,
array<double>^ y,
double time,
double width,
array<double>^ xlocal,
array<double>^ qw,
array<double,2>^ u,
array<double>^ phi,
array<double,2>^ dphi
) |
Parameters
- interval
- Type: System..::.Int32
An int, the index related to the integration interval
[xGrid[interval-1], xGrid[interval]].
- y
- Type: array<
System..::.Double
>[]()[]
An input double array of length 3*xGrid.Length
containing the coefficients of the Hermite quintic spline
representing the solution of the Feynman-Kac equation at time
point time. For each
the approximate solution is locally defined by
The values
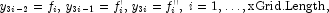 are stored as successive triplets in y.
are stored as successive triplets in y.
- time
- Type: System..::.Double
A double scalar, the time point.
- width
- Type: System..::.Double
A double scalar, the width of the integration interval,
width=xGrid[interval]-xGrid[interval-1].
- xlocal
- Type: array<
System..::.Double
>[]()[]
An input double array containing the Gauss-Legendre points translated and
normalized to the interval [xGrid[interval-1], xGrid[interval]]. The array
length is equal to the degree of the Gauss-Legendre polynomial.
- qw
- Type: array<
System..::.Double
>[]()[]
An input double array containing the Gauss-Legendre weights. The array
length is equal to the degree of the Gauss-Legendre polynomial.
- u
- Type: array<
System..::.Double
,2>[,](,)[,]
An input double matrix of dimension 12 by xlocal.Length
containing the basis function values that define
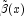 at the Gauss-Legendre
points xlocal. Setting
vector
at the Gauss-Legendre
points xlocal. Setting
vector 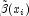 is defined as
is defined as
- phi
- Type: array<
System..::.Double
>[]()[]
An output double array of length 6 containing Gauss-Legendre
approximations for the local contributions
where t=time and
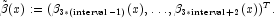 Denoting by degree the number of Gauss-Legendre points (xlocal.Length) and setting
Denoting by degree the number of Gauss-Legendre points (xlocal.Length) and setting
![x_j:=\text{xlocal[j]}](eqn/eqn_1216.png) , vector phi
contains elements
for i=0,...,5.
, vector phi
contains elements
for i=0,...,5.
- dphi
- Type: array<
System..::.Double
,2>[,](,)[,]
An output double matrix of dimension 6 by 6 containing a
Gauss-Legendre approximation for the Jacobian of the local contributions
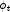 at time point t=time,
The approximation to this symmetric matrix is stored row-wise, i.e.
for i,j=0,...,5.
at time point t=time,
The approximation to this symmetric matrix is stored row-wise, i.e.
for i,j=0,...,5.
 See Also
See Also
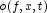 and its derivative
and its derivative 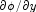 .
.
 Syntax
Syntax![x \in [x_i,x_{i+1}], \, h_i=x_{i+1}-x_i, z_i=(x-x_i)/h_i,\,i=1,\ldots, \text{xGrid.Length}-1](eqn/eqn_1207.png) The values
The values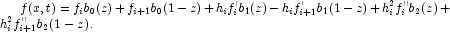
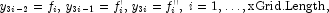 are stored as successive triplets in y.
are stored as successive triplets in y.
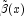 at the Gauss-Legendre
points xlocal. Setting
vector
at the Gauss-Legendre
points xlocal. Setting
vector![u_{k,i}:=\text{u[k,i]} \quad \mbox{and} \quad x_i:=\text{xlocal[i]} \,,](eqn/eqn_1211.png)
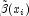 is defined as
is defined as
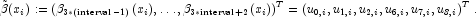
![\phi_t := \int_{\text{xgrid[interval-1]}}^{\text{xgrid[interval]}}\phi(f,x,t)
\tilde{\beta}(x) dx,](eqn/eqn_1214.png)
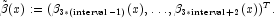 Denoting by degree the number of Gauss-Legendre points (xlocal.Length) and setting
Denoting by degree the number of Gauss-Legendre points (xlocal.Length) and setting
![x_j:=\text{xlocal[j]}](eqn/eqn_1216.png) , vector phi
contains elements
for i=0,...,5.
, vector phi
contains elements
for i=0,...,5.![\text{phi[i]} = \text{width}*\sum_{j=0}^{\text{degree-1}}\text{qw}[j]\,\tilde{\beta}_i(x_j)\,\phi(f,x_j,t)](eqn/eqn_1217.png)
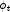 at time point t=time,
The approximation to this symmetric matrix is stored row-wise, i.e.
at time point t=time,
The approximation to this symmetric matrix is stored row-wise, i.e.![\frac{\partial \phi_t}{\partial y}=\int_{\text{xgrid[interval-1]}}^{\text{xgrid[interval]}}
\frac{\partial \phi (f,x,t)}{\partial f} \,\tilde{\beta}(x)\,\tilde{\beta}^T(x)dx\,.](eqn/eqn_1219.png) for i,j=0,...,5.
for i,j=0,...,5.![\text{dphi[i,j]} = \text{width} * \sum_{k=0}^{\text{degree-1}}\text{qw}[k]\,\tilde{\beta}_i(x_k)\,\tilde{\beta}_j(x_k)
\left. \frac{\partial{\phi}}{\partial f}\right|_{x=\text{xlocal}[k],\,t=\text{time}}](eqn/eqn_1220.png)