Detects and determines outliers and simultaneously estimates the model parameters in a time series whose underlying outlier free series follows a general seasonal or nonseasonal ARMA model. This class also allows computation of forecasts.

Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.0.0

Syntax

C#
[SerializableAttribute] public class ARMAOutlierIdentification

Visual Basic (Declaration)
<SerializableAttribute> _ Public Class ARMAOutlierIdentification

Visual C++
[SerializableAttribute] public ref class ARMAOutlierIdentification

Remarks

Consider a univariate time series $\{Y_t\}$ that can be described by the following multiplicative seasonal ARIMA model of order $(p,0,q) \times (0,d,0)_s$ :

$Y_t - \mu = \frac{\theta(B)}{\Delta_s^d \phi(B)} a_t,\, t = 1,\ldots,n$

Here, $\Delta_s^d=(1-B^s)^d,\, \theta(B)=1-\theta_1B-\ldots-\theta_qB^q,\, \phi(B)=1-\phi_1B-\ldots-\phi_pB^p$ . B is the lag operator, $B^kY_t=Y_{t-k}$ , $\{a_t\}$ is a white noise process, and $\mu$ denotes the mean of the series $\{Y_t\}$ .

Outlier detection and parameter estimation

In general, $\{Y_t\}$ is not directly observable due to the influence of outliers. Chen and Liu (1993) distinguish between four types of outliers: innovational outliers (IO), additive outliers (AO), temporary changes (TC) and level shifts (LS). If an outlier occurs as the last observation of the series, then Chen and Liu's algorithm is unable to determine the outlier's classification. In class ARMAOutlierIdentification, such an outlier is called a UI (unable to identify) and is treated as an innovational outlier.

In order to take the effects of multiple outliers occurring at time points $t_1,\ldots,t_m$ into account, Chen and Liu consider the following model:

$Y_t^\ast - \mu = \sum_{j=1}^m\omega_jL_j(B)I_t(t_j)+\frac{\theta(B)}{\Delta_s^d\phi(B)}a_t$

Here, $\{Y_t^\ast\}$ is the observed outlier contaminated series, and $\omega_j$ and

denote the magnitude and dynamic pattern of outlier j, respectively.

is an indicator function that determines the temporal course of the outlier effect, $I_{t_j}(t_j)=1, I_t(t_j)=0$ otherwise. Note that

operates on

via $B^kI_t=I_{t-k}, \, k=0,1,\ldots$ .

The last formula shows that the outlier free series $\{Y_t\}$ can be obtained from the original series $\{Y_t^\ast\}$ by removing all occurring outlier effects:

$Y_t = Y_t^\ast-\sum_{j=1}^m\omega_jL_j(B)I_t(t_j)$

The different types of outliers are characterized by different values for

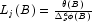$L_j(B)=\frac{\theta(B)}{\Delta_s^d\phi(B)}$ for an innovational outlier,
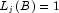for an additive outlier,
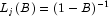$L_j(B)=(1-B)^{-1}$ for a level shift outlier and
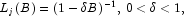$L_j(B)=(1-\delta B)^{-1},\, 0 \lt \delta \lt 1,$ for a temporary change outlier.

Class ARMAOutlierIdentification is an implementation of Chen and Liu's algorithm. It determines the coefficients in $\phi(B)$ and $\theta(B)$ and the outlier effects in the model for the observed series jointly in three stages. The magnitude of the outlier effects is determined by least squares estimates. Outlier detection itself is realized by examination of the maximum value of the standardized statistics of the outlier effects. For a detailed description, see Chen and Liu's original paper (1993).

Intermediate and final estimates for the coefficients in $\phi(B)$ and $\theta(B)$ are computed by the Compute methods from classes ARMA and ARMAMaxLikelihood. If the roots of $\phi(B)$ or $\theta(B)$ lie on or within the unit circle, then the algorithm stops with an appropriate exception. In this case, different values for p and q should be tried.

Forecasting

From the relation between original and outlier free series,

$Y_t^\ast = Y_t+\sum_{j=1}^m\omega_jL_j(B)I_t(t_j)$

it follows that the Box-Jenkins forecast at origin t for lead time l, $\hat{Y}_t^\ast(l)$ , can be computed as

$\hat{Y}_t^\ast(l) = \hat{Y}_t(l)+\sum_{j=1}^m \omega_jL_j(B)I_{t+l}(t_j) ,\; l=1,\ldots,{\rm{nForecast}}$

Therefore, computation of the forecasts for $\{Y^\ast_t\}$ is done in two steps:

Computation of the forecasts for the outlier free series $\{Y_t\}$ .
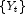Computation of the forecasts for the original series 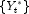$\{Y^\ast_t\}$ by adding the multiple outlier effects to the forecasts for $\{Y_t\}$ .

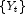Step 1: Computation of the forecasts for the outlier free series $\{Y_t\}$

Since

$\varphi(B)(Y_t-\mu) = \theta(B)a_t$

where

$\varphi(B):=\Delta_s^d\phi(B)=1-\varphi_1B-\ldots-\varphi_{p+sd}B^{p+sd}$

the Box-Jenkins forecast at origin t for lead time l, $\hat{Y}_t(l)$ , can be computed recursively as

$\hat{Y}_t(l)=(1-\sum_{j=1}^{p+sd}\varphi_j)\mu+\sum_{j=1}^{p+sd}\varphi_j\hat{Y}_t(l-j)-\sum_{j=1}^q\theta_ja_{t+l-j}$

Here,

$\hat{Y}_t(l-j)= \left\{ \begin{array}{ccc} Y_{t+l-j} & {\mbox{for}} & l-j \le 0 \\ \hat{Y}_t(l-j) & {\mbox{for}} & l-j \gt 0 \end{array} \right.$

and

$a_k = \left\{ \begin{array}{ccc} 0 & {\mbox{for}} & k \le \max\{1, p+sd\} \\ Y_k-\hat{Y}_{k-1}(1) & {\mbox{for}} & k = \max\{1, p+sd\}+1,\ldots,n \end{array} \right.$

Step 2: Computation of the forecasts for the original series $\{{Y_t}^*\}$ by adding the multiple outlier effects to the forecasts for $\{Y_t\}$

The formulas for for the different types of outliers are as follows:

Innovational outlier (IO)

$L_j(B) = \frac{\theta(B)}{\Delta_s^d\phi(B)}:=\psi(B)=\sum_{k=0}^\infty\psi_kB^k,\, \psi_0=1$

Additive outliers (AO)

Level shifts (LS)

$L_j(B) = \frac{1}{1-B}=\sum_{k=0}^{\infty}B^k$

Temporary changes (TC)

$L_j(B) = \frac{1}{1-\delta B}=\sum_{k=0}^\infty\delta^kB^k$

Assuming the outlier occurs at time point

, the outlier impact is therefore:

Innovational outliers (IO)

$\omega_jL_j(B)I_t(t_j) = \left\{ \begin{array}{ccc} 0 & {\mbox{for}} & t \lt t_j \\ \omega_j \psi_k & {\mbox{for}} & t=t_j+k, \, k \ge 0 \end{array} \right.$

Additive outliers (AO)

$\omega_jL_j(B)I_t(t_j) = \left\{ \begin{array}{ccc} 0 & {\mbox{for}} & t \ne t_j \\ \omega_j & {\mbox{for}} & t=t_j \end{array} \right.$

Level shifts (LS)

$\omega_jL_j(B)I_t(t_j) = \left\{ \begin{array}{ccc} 0 & {\mbox{for}} & t \lt t_j \\ \omega_j & {\mbox{for}} & t=t_j+k, \, k \ge 0 \end{array} \right.$

Temporary changes (TC)

$\omega_jL_j(B)I_t(t_j) = \left\{ \begin{array}{ccc} 0 & {\mbox{for}} & t \lt t_j \\ \omega_j \delta^k & {\mbox{for}} & t=t_j+k, \, k \ge 0 \end{array} \right.$

From these formulas, the forecasts $\hat{Y}_t^\ast(l)$ can be computed easily. The $100(1-\alpha)$ percent probability limits for $Y_{t+l}^\ast$ and $Y_{t+l}$ are given by

$\hat{Y}_t^\ast(l)\, {\rm{(or }}\,\,\, \hat{Y}_t(l) {\rm{, resp.)}} \pm u_{\alpha/2}(1+\sum_{j=1}^{l-1}\psi_j^2)^{1/2}s_a$

where $u_{\alpha/2}$ is the $100(1-\alpha/2)$ percentile of the standard normal distribution,

is an estimate of the variance $\sigma_a^2$ of the random shocks, and the $\psi$ weights $\{\psi_j\}$ are the coefficients in

$\psi(B) := \sum_{k=0}^\infty \psi_k B^k := \frac{\theta(B)}{\Delta_s^d\phi(B)}, \, \psi_0=1 \,.$

For a detailed explanation of these concepts, see chapter 5:"Forecasting" in Box, Jenkins and Reinsel (1994).

Inheritance Hierarchy

System..::.Object
Imsl.Stat..::.ARMAOutlierIdentification

Syntax

Remarks

Inheritance Hierarchy

See Also