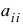CHNNDFAC Procedure (PV-WAVE Advantage)
Computes the Cholesky factorization of the real matrix A such that A = RTR = LLT.
Usage
CHNNDFAC, a, fac
Input Parameters
a—Two-dimensional matrix containing the coefficient matrix. Element A(i, j) contains the jth coefficient of the ith equation.
Output Parameters
fac—Matrix containing the LLT factorization of A.
Input Keywords
Double—If present and nonzero, double precision is used.
Tolerance—Used in determining linear dependence. Default: Tolerance = 100 ε, where ε is machine precision
Output Keywords
Inverse—Specifies a named variable into which the inverse of the matrix A is stored.
Discussion
The factorization algorithm is based on the work of Healy (1968) and proceeds sequentially by columns. The ith column is declared to be linearly dependent on the first i – 1 columns if:
where ε (specified in Tolerance) may be set by the user. When a linear dependence is declared, all elements in the ith row of R (column of L) are set to zero.
Modifications due to Farebrother and Berry (1974) and Barrett and Healy (1978) for checking for matrices that are not nonnegative definite also are incorporated. The CHNNDFAC procedure declares A to not be nonnegative definite and issues an error message if either of the following conditions is satisfied:
1. 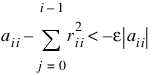
2. 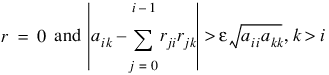
Healy’s (1968) algorithm and the CHNNDFAC procedure permit the matrices A and R to occupy the same storage. Barrett and Healy (1978) in their remark neglect this fact. Procedure CHNNDFAC uses:
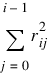
for
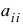
in condition 2 above to remedy this problem.
If an inverse of the matrix A is required and the matrix is not (numerically) positive definite, then the resulting inverse is a symmetric g2 inverse of A. For a matrix G to be a g2 inverse of a matrix A, G must satisfy conditions 1 and 2 for the Moore-Penrose inverse but generally fail conditions 3 and 4. The four conditions for G to be a Moore-Penrose inverse of A are as follows:
1. AGA = A
2. GAG = G
3. AG is symmetric
4. GA is symmetric
Example
The symmetric nonnegative definite matrix in the initial example of CHNNDSOL is used to compute the factorization only in the first call to CHNNDFAC. Then, CHNNDSOL is called with both the LLT factorization and the right-hand side vector as the input to compute a solution x.
; Define the coefficient matrix.
RM, a, 4, 4
row 0: 36 12 30 6
row 1: 12 20 2 10
row 2: 30 2 29 1
row 3: 6 10 1 14
CHNNDFAC, a, fac
PM, fac, Title = 'Factor', Format = '(4f12.3)'
; PV-WAVE prints the following:
; Factor
; 6.000 2.000 5.000 1.000
; 2.000 4.000 -2.000 2.000
; 5.000 -2.000 0.000 0.000
; 1.000 2.000 0.000 3.000
; Define the right-hand side.
RM, b, 4, 1
row 0: 18
row 1: 22
row 2: 7
row 3: 20
; Compute the solution and output.
x = CHNNDSOL(b, Factor = fac)
PM, x, Title = 'Solution'
; PV-WAVE prints the following:
; Solution
; 0.166667
; 0.500000
; 0.00000
; 1.00000
Warning Errors
MATH_INCONSISTENT_EQUATIONS_2—Linear system of equations is inconsistent.
MATH_NOT_NONNEG_DEFINITE—Matrix A is not nonnegative definite.
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.
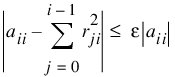
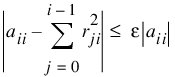
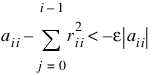
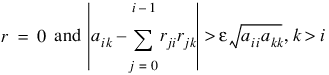
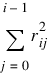 for
for