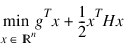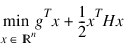QUADPROG Function (PV-WAVE Extreme Advantage)
Solves a quadratic programming (QP) problem subject to linear equality or inequality constraints.
Usage
result = QUADPROG(a, b, g, h)
Input Parameters
a—A two-dimensional matrix containing the linear constraints.
b—A one-dimensional matrix of the right-hand sides of the linear constraints.
g—A one-dimensional array of the coefficients of the linear term of the objective function.
h—A two-dimensional array of size N_ELEMENTS(g)-by-N_ELEMENTS(g) containing the Hessian matrix of the objective function. The array must be symmetric positive definite. If h is not positive definite, the algorithm attempts to solve the QP problem with h replaced by h + diag*1, such that h + diag*1 is positive definite.
Returned Value
result —The solution to the QP problem.
Keywords
Diag—The name of the variable into which the scalar, equal to the multiple of the identity matrix added to h to give a positive definite matrix, is stored.
Double—If present and nonzero, double precision is used in the computation.
Dual—The name of the variable into which an array with N_ELEMENTS(g) elements, containing the Lagrange multiplier estimates, is stored.
Meq—The number of linear equality constraints. If Meq is used, the equality constraints are located at A (i, *) for i = 0, …, Meq – 1.
(Default: Meq = N_ELEMENTS(A (*, 0) ) n; i.e., all constraints are equality constraints)
Obj—The name of the variable into which the optimal object function is stored.
Discussion
QUADPROG is based on M.J.D. Powell’s implementation of the Goldfarb and Idnani dual quadratic programming (QP) algorithm for convex QP problems subject to general linear equality/inequality constraints (Goldfarb and Idnani, 1983). These problems are of the form:
subject to:
A1x = b1
A2x ≥ b2
given the arrays b0, b1, and g, and the matrices H, A0, and A1. Matrix H is required to be positive definite. In this case, a unique x solves the problem, or the constraints are inconsistent. If H is not positive definite, a positive definite perturbation of H is used in place of H . For more details, see Powell (1983, 1985).
If a perturbation of H, H + αI, is used in the QP problem, H + αI also should be used in the definition of the Lagrange multipliers.
Example
The QP problem:
min f(x) = x02 + x12 + x22 + x32 + x42 – 2x1x2 – 2x3x4 –2x0
subject to:
x0 + x1 + x2 + x3 + x4 = 5
x2 – 2x3 – 2x4 = –3
is solved.
; Define the coefficient matrix A.
RM, a, 2, 5
row 0: 1 1 1 1 1
row 1: 0 0 1 -2 -2
; Define the Hessian matrix of the objective function. Notice
; that since h is symmetric, the array concatenation
; operators “[ ]” are used in its definition.
h = [[2, 0, 0, 0, 0], [0, 2, -2, 0, 0], $
[0, -2, 2, 0, 0], [0, 0, 0, 2, -2], $
; [0, 0, 0, -2, 2]]
b = [5, -3]
g = [ -2, 0, 0, 0, 0]
x = QUADPROG(a, b, g, h)
PM, x
; PV-WAVE prints the following:
; 1.00000
; 1.00000
; 1.00000
; 1.00000
; 1.00000
For Additional Information
Goldfarb and Idnani, 1983.
Powell, 1983 and 1985.
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.