- java.lang.Object
-
- com.imsl.math.MinUncon
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class MinUncon extends Object implements Serializable, Cloneable
Unconstrained minimization.MinUnconuses two separate algorithms to compute the minimum depending on what the user supplies as the functionf.If
fdefines the function whose minimum is to be foundMinUnconuses a safeguarded quadratic interpolation method to find a minimum point of a univariate function. Both the code and the underlying algorithm are based on the routineZXLSFwritten by M.J.D. Powell at the University of Cambridge.MinUnconfinds the least value of a univariate function, f, wherefimplementsMinUnconFunction f. Optional data include an initial estimate of the solution, and a positive numberbound, specified by thesetBoundmethod. Let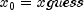 where
where xguessis specified by thesetGuessmethod and b = bound, then x is restricted to the interval![[x_0 - b, x_0 + b]](eqn_1050.png) . Usually, the algorithm begins the
search by moving from
. Usually, the algorithm begins the
search by moving from 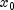 to
to 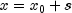 ,
where s = step.
,
where s = step. stepis set by thesetStepmethod. IfsetStepis not called thenstepis set to 0.1.stepmay be positive or negative. The first two function evaluations indicate the direction to the minimum point, and the search strides out along this direction until a bracket on a minimum point is found or until x reaches one of the bounds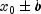 .
During this stage, the step length increases by a factor of between two and
nine per function evaluation; the factor depends on the position of the
minimum point that is predicted by quadratic interpolation of the three most
recent function values.
.
During this stage, the step length increases by a factor of between two and
nine per function evaluation; the factor depends on the position of the
minimum point that is predicted by quadratic interpolation of the three most
recent function values.When an interval containing a solution has been found, we will have three points,
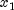 ,
, 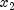 , and
, and
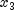 , with
, with 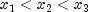 and
and
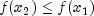 and
and 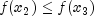 .
There are three main ingredients in the technique for choosing the new
x from these three points. They are (i) the estimate of
the minimum point that is given by quadratic interpolation of the three
function values, (ii) a tolerance parameter
.
There are three main ingredients in the technique for choosing the new
x from these three points. They are (i) the estimate of
the minimum point that is given by quadratic interpolation of the three
function values, (ii) a tolerance parameter  ,
that depends on the closeness of f to a quadratic, and
(iii) whether
,
that depends on the closeness of f to a quadratic, and
(iii) whether 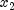 is near the center of the range between
is near the center of the range between
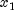 and
and 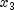 or is relatively close
to an end of this range. In outline, the new value of x
is as near as possible to the predicted minimum point, subject to being at
least
or is relatively close
to an end of this range. In outline, the new value of x
is as near as possible to the predicted minimum point, subject to being at
least  from
from 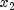 , and
subject to being in the longer interval between
, and
subject to being in the longer interval between 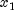 and
and
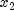 or
or 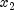 and
and
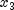 when
when 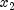 is particularly
close to
is particularly
close to 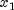 or
or 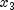 . There is some
elaboration, however, when the distance between these points is close to the
required accuracy; when the distance is close to the machine precision; or
when
. There is some
elaboration, however, when the distance between these points is close to the
required accuracy; when the distance is close to the machine precision; or
when  is relatively large.
is relatively large.The algorithm is intended to provide fast convergence when f has a positive and continuous second derivative at the minimum and to avoid gross inefficiencies in pathological cases, such as
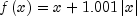
The algorithm can make
 large automatically
in the pathological cases. In this case, it is usual for a new value of
x to be at the midpoint of the longer interval that is
adjacent to the least calculated function value. The midpoint strategy is used
frequently when changes to f are dominated by
computer rounding errors, which will
almost certainly happen if the user requests an accuracy that is less than
the square root of the machine precision. In such cases, the routine claims
to have achieved the required accuracy if it knows that there is a local
minimum point within distance
large automatically
in the pathological cases. In this case, it is usual for a new value of
x to be at the midpoint of the longer interval that is
adjacent to the least calculated function value. The midpoint strategy is used
frequently when changes to f are dominated by
computer rounding errors, which will
almost certainly happen if the user requests an accuracy that is less than
the square root of the machine precision. In such cases, the routine claims
to have achieved the required accuracy if it knows that there is a local
minimum point within distance 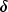 of
x, where
of
x, where 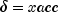 , specified
by the
, specified
by the setAccuracymethod even though the rounding errors in f may cause the existence of other local minimum points nearby. This difficulty is inevitable in minimization routines that use only function values, so high precision arithmetic is recommended.If
fimplementsMinUnconDerivativethenMinUnconuses a descent method with either the secant method or cubic interpolation to find a minimum point of a univariate function. It starts with an initial guess and two endpoints. If any of the three points is a local minimum point and has least function value, the routine terminates with a solution. Otherwise, the point with least function value will be used as the starting point.From the starting point, say
 , the function value
, the function value
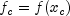 , the derivative value
, the derivative value
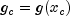 , and a new point
, and a new point 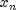 defined by
defined by 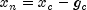 are computed. The function
are computed. The function
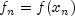 , and the derivative
, and the derivative
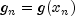 are then evaluated. If either
are then evaluated. If either
 or
or 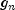 has the opposite
sign of
has the opposite
sign of 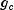 , then there exists a minimum point between
, then there exists a minimum point between
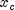 and
and 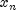 ; and an initial
interval is obtained. Otherwise, since
; and an initial
interval is obtained. Otherwise, since 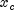 is kept as
the point that has lowest function value, an interchange between
is kept as
the point that has lowest function value, an interchange between
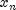 and
and 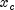 is performed. The
secant method is then used to get a new point
is performed. The
secant method is then used to get a new point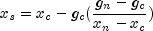
Let
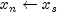 and repeat this process until
an interval containing a minimum is found or one of the convergence criteria
is satisfied. The convergence criteria are as follows: Criterion 1:
and repeat this process until
an interval containing a minimum is found or one of the convergence criteria
is satisfied. The convergence criteria are as follows: Criterion 1: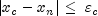
Criterion 2:
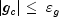
where
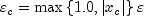 ,
,  is a
relative error tolerance and
is a
relative error tolerance and  is a
gradient tolerance.
is a
gradient tolerance. When convergence is not achieved, a cubic interpolation is performed to obtain a new point. Function and derivative are then evaluated at that point; and accordingly, a smaller interval that contains a minimum point is chosen. A safeguarded method is used to ensure that the interval reduces by at least a fraction of the previous interval. Another cubic interpolation is then performed, and this procedure is repeated until one of the stopping criteria is met.
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static interfaceMinUncon.DerivativePublic interface for the user supplied function to theMinUnconobject.static interfaceMinUncon.FunctionPublic interface for the user supplied function to theMinUnconobject.
-
Constructor Summary
Constructors Constructor and Description MinUncon()Unconstrained minimum constructor for a smooth function of a single variable of typedouble.
-
Method Summary
Methods Modifier and Type Method and Description doublecomputeMin(MinUncon.Function F)Return the minimum of a smooth function of a single variable of typedoubleusing function values only or using function values and derivatives.voidsetAccuracy(double xacc)Set the required absolute accuracy in the final value returned by member functioncomputeMin.voidsetBound(double bound)Set the amount by which X may be changed from its initial value, xguess.voidsetDerivtol(double gtol)Set the derivative tolerance used by member functioncomputeMinto decide if the current point is a local minimum.voidsetGuess(double xguess)Set the initial guess of the minimum point of the input function.voidsetStep(double step)Set the stepsize to use when changing x.
-
-
-
Constructor Detail
-
MinUncon
public MinUncon()
Unconstrained minimum constructor for a smooth function of a single variable of typedouble.
-
-
Method Detail
-
computeMin
public double computeMin(MinUncon.Function F)
Return the minimum of a smooth function of a single variable of typedoubleusing function values only or using function values and derivatives.- Parameters:
F- defines the function whose minimum is to be found. IfFimplementsDerivativethen derivatives are used. Otherwise, an attempt to find the minimum is made using function values only.- Returns:
- a
doublescalar value containing the minimum of the input function
-
setAccuracy
public void setAccuracy(double xacc)
Set the required absolute accuracy in the final value returned by member functioncomputeMin. If this member function is not called, the required accuracy is set to 1.0e-8.- Parameters:
xacc- adoublescalar value specifying the required absolute accuracy in the final value returned by member functioncomputeMin.
-
setBound
public void setBound(double bound)
Set the amount by which X may be changed from its initial value, xguess. If this member function is not called, bound is set to 100.- Parameters:
bound- adoublescalar value specifying the amount by which X may be changed from its initial value. In other words, X is restricted to the interval [xguess-bound,xguess+bound].
-
setDerivtol
public void setDerivtol(double gtol)
Set the derivative tolerance used by member functioncomputeMinto decide if the current point is a local minimum. This is the second stopping criterion. x is returned as a solution when G(x) is less than or equal togtol.gtolshould be nonnegative, otherwise zero will be used. If this member function is not called, the derivative tolerance is set to 1.0e-8.- Parameters:
gtol- adoublescalar value specifying the derivative tolerance used by member functioncomputeMin.
-
setGuess
public void setGuess(double xguess)
Set the initial guess of the minimum point of the input function. If this member function is not called, an initial guess of 0.0 is used.- Parameters:
xguess- adoublescalar value specifying the initial guess of the minimum point of the input function
-
setStep
public void setStep(double step)
Set the stepsize to use when changing x. If this member function is not called, step is set to 0.1.- Parameters:
step- adoublescalar value specifying the order of magnitude estimate of the required change in x when stepping towards the minimum
-
-