- java.lang.Object
-
- com.imsl.math.Quadrature
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class Quadrature extends Object implements Serializable, Cloneable
Quadratureis a general-purpose integrator that uses a globally adaptive scheme in order to reduce the absolute error. It subdivides the interval [A, B] and uses a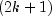 -point
Gauss-Kronrod rule to estimate the integral over each subinterval. The
error for each subinterval is estimated by comparison with the k-point
Gauss quadrature rule. The subinterval with the largest estimated error is
then bisected and the same procedure is applied to both halves. The
bisection process is continued until either the error criterion is satisfied,
roundoff error is detected, the subintervals become too small, or the
maximum number of subintervals allowed is reached. The Class
-point
Gauss-Kronrod rule to estimate the integral over each subinterval. The
error for each subinterval is estimated by comparison with the k-point
Gauss quadrature rule. The subinterval with the largest estimated error is
then bisected and the same procedure is applied to both halves. The
bisection process is continued until either the error criterion is satisfied,
roundoff error is detected, the subintervals become too small, or the
maximum number of subintervals allowed is reached. The Class Quadratureis based on the subroutineQAGby Piessens et al. (1983).If the function to be integrated has endpoint singularities then extrapolation should be enabled. As described above, the integral's value is approximated by applying a quadrature rule to a series of subdivisions of the interval. The sequence of approximate values converges to the integral's value. The
 -algorithm can be used to extrapolate from
the initial terms of the sequence to its limit.
Without extrapolation, the quadrature approximation sequence converges slowly
if the function being integrated has endpoint singularities.
The
-algorithm can be used to extrapolate from
the initial terms of the sequence to its limit.
Without extrapolation, the quadrature approximation sequence converges slowly
if the function being integrated has endpoint singularities.
The  -algorithm accelerates convergence of the sequence in this case.
The class
-algorithm accelerates convergence of the sequence in this case.
The class EpsilonAlgorithmimplements the -algorithm.
With extrapolation, this class is similar to the subroutine
-algorithm.
With extrapolation, this class is similar to the subroutine QAGSby Piessens et al. (1983).The desired absolute error,
 , can be set using
, can be set using setAbsoluteError. The desired relative error,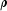 , can be set using
, can be set using setRelativeError. The methodevalcomputes the approximate integral value .
It also computes an error estimate E, which can be retrieved using
.
It also computes an error estimate E, which can be retrieved using getErrorEstimate. These are related by the following equation: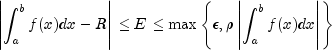
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static interfaceQuadrature.FunctionPublic interface function for the Quadrature class.
-
Constructor Summary
Constructors Constructor and Description Quadrature()Constructs a Quadrature object.
-
Method Summary
Methods Modifier and Type Method and Description doubleeval(Quadrature.Function objectF, double a, double b)Returns the value of the integral from a to b.doublegetErrorEstimate()Returns an estimate of the relative error in the computed result.intgetErrorStatus()Returns the non-fatal error status.voidsetAbsoluteError(double errorAbsolute)Sets the absolute error tolerance.voidsetExtrapolation(boolean doExtrapolation)If true, the epsilon-algorithm for extrapolation is enabled.voidsetMaxSubintervals(int maxSubintervals)Sets the maximum number of subintervals allowed.voidsetRelativeError(double errorRelative)Sets the relative error tolerance.voidsetRule(int rule)Set the Gauss-Kronrod rule.
-
-
-
Method Detail
-
eval
public double eval(Quadrature.Function objectF, double a, double b)
Returns the value of the integral from a to b.- Parameters:
objectF- an implementation ofFunctioncontaining the function to be integrateda- adoublespecifying the lower limit of integrationb- adoublespecifying the upper limit of integration, either or both of a and b can be Double.POSITIVE_INFINITY or Double.NEGATIVE_INFINITY
-
getErrorEstimate
public double getErrorEstimate()
Returns an estimate of the relative error in the computed result.- Returns:
- a
doublespecifying an estimate of the relative error in the computed result
-
getErrorStatus
public int getErrorStatus()
Returns the non-fatal error status.- Returns:
- an
intspecifying the non-fatal error status:Status Meaning 0 No error. 1 Maximum number of subdivisions allowed has been achieved. One can allow more subdivisions by using setMaxSubintervals. If this yields no improvement it is advised to analyze the integrand in order to determine the integration difficulties. If the position of a local difficulty can be determined (e.g. singularity, discontinuity within the interval) one will probably gain from splitting up the interval at this point and calling the integrator on the subranges. If possible, an appropriate special-purpose integrator should be used, which is designed for handling the type of difficulty involved. 2 The occurrence of roundoff error is detected, which prevents the requested tolerance from being achieved. The error may be under-estimated. 3 Extremely bad integrand behavior occurs at some points of the integration interval. 4 The algorithm does not converge. Roundoff error is detected in the extrapolation table. It is presumed that the requested tolerance cannot be achieved, and that the returned result is the best which can be obtained. 5 The algorithm does not converge. Roundoff error is detected in the extrapolation table. It is presumed that the requested tolerance cannot be achieved, and that the returned result is the best that can be obtained. 6 The integral is probably divergent, or slowly convergent. It must be noted that divergence can occur with any other status value.
-
setAbsoluteError
public void setAbsoluteError(double errorAbsolute)
Sets the absolute error tolerance.- Parameters:
errorAbsolute- adoublescalar value specifying the absolute error tolerance. The default value is 1.0536712127723714E-8.
-
setExtrapolation
public void setExtrapolation(boolean doExtrapolation)
If true, the epsilon-algorithm for extrapolation is enabled. The default is false (extrapolation is not used).- Parameters:
doExtrapolation- aboolean, true if the epsilon-algorithm for extrapolation is to be enabled, false otherwise
-
setMaxSubintervals
public void setMaxSubintervals(int maxSubintervals)
Sets the maximum number of subintervals allowed. The default value is 500.- Parameters:
maxSubintervals- anintspecifying the maximum number of subintervals to be allowed. The default is 500.
-
setRelativeError
public void setRelativeError(double errorRelative)
Sets the relative error tolerance.- Parameters:
errorRelative- adoublescalar value specifying the relative error tolerance. The default value is 1.0536712127723714E-8.
-
setRule
public void setRule(int rule)
Set the Gauss-Kronrod rule.
The default is rule 3.Rule Data points used 1 7 - 15 2 10 - 21 3 15 - 31 4 20 - 41 5 25 - 51 6 30 - 61 - Parameters:
rule- anintspecifying the rule to be used. The default is 3.
-
-