-
- Enclosing class:
- FeynmanKac
public static interface FeynmanKac.ForcingTermPublic interface for non-zero forcing term in the Feynman-Kac equation.
-
-
Method Summary
Methods Modifier and Type Method and Description voidforce(int interval, double[] y, double time, double width, double[] xlocal, double[] qw, double[][] u, double[] phi, double[][] dphi)Computes approximations to the forcing term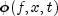 and its derivative
and its derivative 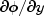 .
.
-
-
-
Method Detail
-
force
void force(int interval, double[] y, double time, double width, double[] xlocal, double[] qw, double[][] u, double[] phi, double[][] dphi)Computes approximations to the forcing term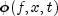 and its derivative
and its derivative 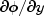 .
.- Parameters:
interval- anint, the index related to the integration interval[xGrid[interval-1], xGrid[interval]].y- an inputdoublearray of length3*xGrid.lengthcontaining the coefficients of the Hermite quintic spline representing the solution of the Feynman-Kac equation at time pointtime. For each
the approximate solution is locally defined by![x in [x_i,x_{i+1}], , h_i=x_{i+1}-x_i, z_i=(x-x_i)/h_i,,i=1,ldots, text{xGrid.length}-1](eqn_1385.png)
The values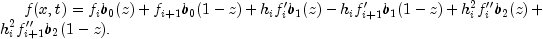
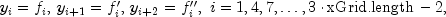 are stored as successive triplets in
are stored as successive triplets in y.time- adouble, the time point.width- adouble, the width of the integration interval,width=xGrid[interval]-xGrid[interval-1].xlocal- an inputdoublearray containing the Gauss-Legendre points translated and normalized to the interval[xGrid[interval-1], xGrid[interval]].qw- an inputdoublearray containing the Gauss-Legendre weights.u- an inputdoublearray of dimension12 by xlocal.lengthcontaining the basis function values that define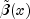 at the Gauss-Legendre
points
at the Gauss-Legendre
points xlocal. Setting
vector![u_{k,i}:=text{u[k][i]} quad mbox{and} quad x_i:=text{xlocal[i]} ,,](eqn_1389.png)
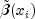 is defined as
is defined as
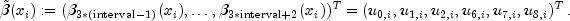
phi- an outputdoublearray of length 6 containing Gauss-Legendre approximations for the local contributions
where![phi_t := int_{text{xgrid[interval-1]}}^{text{xgrid[interval]}}phi(f,x,t)
tilde{beta}(x) dx,](eqn_1392.png)
t=timeand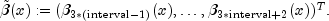 Denoting by
Denoting by degreethe number of Gauss-Legendre points (xlocal.length) and setting![x_j:=text{xlocal[j]}](eqn_1394.png) , vector
, vector phicontains elements
for![text{phi[i]} = text{width}*sum_{j=0}^{text{degree-1}}text{qw}[j],tilde{beta}_i(x_j),phi(f,x_j,t)](eqn_1395.png)
i=0,...,5.dphi- an outputdoublearray of dimension6 by 6containing a Gauss-Legendre approximation for the Jacobian of the local contributions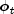 at time point
at time point t=time,
The approximation to this symmetric matrix is stored row-wise, i.e.![frac{partial phi_t}{partial y}=int_{text{xgrid[interval-1]}}^{text{xgrid[interval]}}
frac{partial phi (f,x,t)}{partial f} ,tilde{beta}(x),tilde{beta}^T(x)dx,.](eqn_1397.png)
for![text{dphi[i][j]} = text{width} * sum_{k=0}^{text{degree-1}}text{qw}[k],tilde{beta}_i(x_k),tilde{beta}_j(x_k)
left. frac{partial{phi}}{partial f}right|_{x=text{xlocal}[k],,t=text{time}}](eqn_1398.png)
i,j=0,...,5.
-
-