- java.lang.Object
-
- com.imsl.math.FeynmanKac
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class FeynmanKac extends Object implements Serializable, Cloneable
Solves the generalized Feynman-Kac PDE.Class
FeynmanKacsolves the generalized Feynman-Kac PDE on a rectangular grid with boundary conditions using a finite element Galerkin method. The generalized Feynman-Kac differential equation has the form
where the initial data satisfies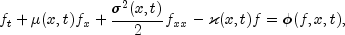
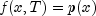 . The derivatives are
. The derivatives are
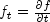 , etc. Method
, etc. Method
computeCoefficientsuses a finite element Galerkin method over the rectangle
in![[x_{min},x_{max}] times [bar{T},T]](eqn_1312.png)
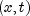 to compute the approximate solution. The interval
to compute the approximate solution. The interval
![[x_{min},x_{max}]](eqn_1314.png) is decomposed with a grid
is decomposed with a grid
On each subinterval the solution is represented by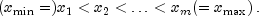
The values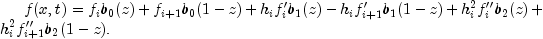
are time-dependent coefficients associated with each interval. The basis functions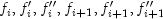
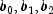 are given for
are given for
by![x in [x_i, x_{i+1}], , h_i=x_{i+1}-x_i, , z=(x-x_i)/h_i, z in [0,1],](eqn_1319.png)
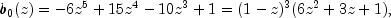
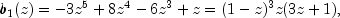
By adding the piece-wise definitions the unknown solution function may be arranged as the series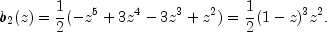
where the time-dependent coefficients are defined by re-labeling:![f(x,t) = sum_{i=1}^{3m}y_ibeta_i(x), ; x in [x_{min},x_{max}],](eqn_1323.png)
The Galerkin principle is then applied. Using the provided initial and boundary conditions leads to an Index 1 differential-algebraic equation for the coefficients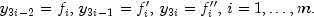
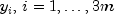 .
.
This system is integrated using the variable order, variable step algorithm
DDASLXnoted in Hanson, R. and Krogh, F. (2008), Solving Constrained Differential-Algebraic Systems Using Projections. Solution values and their time derivatives at a grid preceding time T, expressed in units of time remaining, are given back by methodsgetSplineCoefficientsandgetSplineCoefficientsPrime, respectively. For further details of deriving and solving the system see Hanson, R. (2008), Integrating Feynman-Kac Equations Using Hermite Quintic Finite Elements. To evaluate f or its partials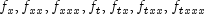 at any
time point in the grid, use method
at any
time point in the grid, use method getSplineValue.One useful application of the
FeynmanKacclass is financial analytics. This is illustrated in Example 2, which solves a diffusion model for call options which, in the special case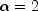 reduces to the Black-Scholes (BS) model.
Another useful application for the
reduces to the Black-Scholes (BS) model.
Another useful application for the FeynmanKacclass is the calculation of the Greeks, i.e. various derivatives of Feynman-Kac solutions applicable to, e.g., the pricing of options and related financial derivatives. In Example 5, theFeynmanKacclass is used to calculate eleven of the Greeks for the same diffusion model introduced in Example 2 in the special BS case. These Greeks are also calculated using the BS closed form Greek equations (see http://en.wikipedia.org/wiki/The_Greeks). The Feynman-Kac and BS solutions are output and compared. Example 5 illustrates that theFeynmanKacclass can be used to explore the Greeks for a much wider class of financial models than can BS.
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static interfaceFeynmanKac.BoundariesPublic interface for user supplied boundary coefficients and terminal condition the PDE must satisfy.static classFeynmanKac.BoundaryInconsistentExceptionThe boundary conditions are inconsistent.static classFeynmanKac.ConstraintsInconsistentExceptionThe constraints are inconsistent.static classFeynmanKac.CorrectorConvergenceExceptionCorrector failed to converge.static classFeynmanKac.ErrorTestExceptionError test failure detected.static interfaceFeynmanKac.ForcingTermPublic interface for non-zero forcing term in the Feynman-Kac equation.static classFeynmanKac.InitialConstraintsExceptionThe constraints at the initial point are inconsistent.static interfaceFeynmanKac.InitialDataPublic interface for adjustment of initial data or as an opportunity for output during the integration steps.static classFeynmanKac.IterationMatrixSingularExceptionIteration matrix is singular.static interfaceFeynmanKac.PdeCoefficientsPublic interface for user supplied PDE coefficients in the Feynman-Kac PDE.static classFeynmanKac.TcurrentTstopInconsistentExceptionThe end value for the integration in time, tout, is not consistent with the current time value, t.static classFeynmanKac.TEqualsToutExceptionThe current integration point in time and the end point are equal.static classFeynmanKac.TimeIntervalTooSmallExceptionDistance between starting time point and end point for the integration is too small.static classFeynmanKac.ToleranceTooSmallExceptionTolerance is too small.static classFeynmanKac.TooManyIterationsExceptionToo many iterations required by the DAE solver.
-
Field Summary
Fields Modifier and Type Field and Description static intMETHOD_OF_PETZOLDUsed by methodsetStepControlMethodto indicate that the step control algorithm of the original Petzold code is used in the integration.static intMETHOD_OF_SOEDERLINDUsed by methodsetStepControlMethodto indicate that the step control method by Soederlind is used in the integration.
-
Constructor Summary
Constructors Constructor and Description FeynmanKac(FeynmanKac.PdeCoefficients pdeCoeffs)Constructs a PDE solver to solve the Feynman-Kac PDE.
-
Method Summary
Methods Modifier and Type Method and Description voidcomputeCoefficients(int numLeftBounds, int numRightBounds, FeynmanKac.Boundaries pdeBounds, double[] xGrid, double[] tGrid)Determines the coefficients of the Hermite quintic splines that represent an approximate solution for the Feynman-Kac PDE.double[]getAbsoluteErrorTolerances()Returns absolute error tolerances.intgetGaussLegendreDegree()Returns the number of quadrature points used in the Gauss-Legendre quadrature formula.doublegetInitialStepsize()Returns the starting step size for the integration.intgetMaximumBDFOrder()Returns the maximum order of the BDF formulas.doublegetMaximumStepsize()Returns the maximum internal step size used by the integrator.intgetMaxSteps()Returns the maximum number of internal steps allowed.double[]getRelativeErrorTolerances()Returns relative error tolerances.double[][]getSplineCoefficients()Returns the coefficients of the Hermite quintic splines that represent an approximate solution of the Feynman-Kac PDE.double[][]getSplineCoefficientsPrime()Returns the first derivatives of the Hermite quintic spline coefficients that represent an approximate solution of the Feynman-Kac PDE.double[]getSplineValue(double[] evaluationPoints, double[] coefficients, int ideriv)Evaluates for time value 0 or a time value in tGrid the derivative of the Hermite quintic spline interpolant at evaluation points within the range ofxGrid.intgetStepControlMethod()Returns the step control method used in the integration of the Feynman-Kac PDE.doublegetTimeBarrier()Returns the barrier set for integration in the time direction.voidsetAbsoluteErrorTolerances(double atol)Sets the absolute error tolerances.voidsetAbsoluteErrorTolerances(double[] atol)Sets the absolute error tolerances.voidsetForcingTerm(FeynmanKac.ForcingTerm forceTerm)Sets the user-supplied method that computes approximations to the forcing term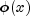 and its derivative
and its derivative 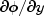 used in the FeynmanKac PDE.
used in the FeynmanKac PDE.voidsetGaussLegendreDegree(int degree)Sets the number of quadrature points used in the Gauss-Legendre quadrature formula.voidsetInitialData(FeynmanKac.InitialData initData)Sets the user-supplied method for adjustment of initial data or as an opportunity for output during the integration steps.voidsetInitialStepsize(double initStepsize)Sets the starting stepsize for the integration.voidsetMaximumBDFOrder(int maxBDFOrder)Sets the maximum order of the BDF formulas.voidsetMaximumStepsize(double maximumStepsize)Sets the maximum internal step size used by the integrator.voidsetMaxSteps(int maxSteps)Sets the maximum number of internal steps allowed.voidsetRelativeErrorTolerances(double rtol)Sets the relative error tolerances.voidsetRelativeErrorTolerances(double[] rtol)Sets the relative error tolerances.voidsetStepControlMethod(int stepControlMethod)Sets the step control method used in the integration of the Feynman-Kac PDE.voidsetTimeBarrier(double timeBarrier)Sets a barrier for the integration in the time direction.voidsetTimeDependence(boolean[] timeFlag)Sets the time dependence of the coefficients, boundary conditions and function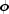 in the Feynman Kac equation.
in the Feynman Kac equation.
-
-
-
Field Detail
-
METHOD_OF_PETZOLD
public static final int METHOD_OF_PETZOLD
Used by methodsetStepControlMethodto indicate that the step control algorithm of the original Petzold code is used in the integration.- See Also:
- Constant Field Values
-
METHOD_OF_SOEDERLIND
public static final int METHOD_OF_SOEDERLIND
Used by methodsetStepControlMethodto indicate that the step control method by Soederlind is used in the integration.- See Also:
- Constant Field Values
-
-
Constructor Detail
-
FeynmanKac
public FeynmanKac(FeynmanKac.PdeCoefficients pdeCoeffs)
Constructs a PDE solver to solve the Feynman-Kac PDE.- Parameters:
pdeCoeffs- Implementation of interface PdeCoefficients that computes the values of the Feynman-Kac coefficients at a given point(t,x).
-
-
Method Detail
-
computeCoefficients
public void computeCoefficients(int numLeftBounds, int numRightBounds, FeynmanKac.Boundaries pdeBounds, double[] xGrid, double[] tGrid) throws FeynmanKac.ToleranceTooSmallException, FeynmanKac.TooManyIterationsException, FeynmanKac.ErrorTestException, FeynmanKac.CorrectorConvergenceException, FeynmanKac.IterationMatrixSingularException, FeynmanKac.TimeIntervalTooSmallException, FeynmanKac.TcurrentTstopInconsistentException, FeynmanKac.TEqualsToutException, FeynmanKac.InitialConstraintsException, FeynmanKac.ConstraintsInconsistentException, SingularMatrixException, FeynmanKac.BoundaryInconsistentExceptionDetermines the coefficients of the Hermite quintic splines that represent an approximate solution for the Feynman-Kac PDE.- Parameters:
numLeftBounds- anint, the number of left boundary conditions. It is required that
1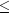
numLeftBounds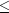
3.numRightBounds- anint, the number of right boundary conditions. It is required that
1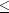
numRightBounds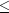
3.pdeBounds- Implementation of interface Boundaries that computes the boundary coefficients and terminal condition for given(t,x).xGrid- adoublearray containing the breakpoints for the Hermite quintic splines used in thexdiscretization. The length ofxGridmust be at least 2,xGrid.length >= 2, and the elements inxGridmust be in strictly increasing order.tGrid- adoublearray containing the set of time points (in time-remaining units) where an approximate solution is returned. The elements in arraytGridmust be positive and in strictly increasing order.- Throws:
FeynmanKac.ToleranceTooSmallException- is thrown if the absolute or relative error tolerances used in the integrator are too small.FeynmanKac.TooManyIterationsException- is thrown if the integrator needs too many iteration steps.FeynmanKac.ErrorTestException- is thrown if the error test used in the integrator failed repeatedly.FeynmanKac.CorrectorConvergenceException- is thrown if the corrector failed to converge repeatedly.FeynmanKac.IterationMatrixSingularException- thrown if one of the iteration matrices used in the integrator is singular.FeynmanKac.TimeIntervalTooSmallException- is thrown if the distance between an intermediate starting and end point for the integration is too small.FeynmanKac.TcurrentTstopInconsistentException- is thrown if during the integration the current integration time and given stepsize is inconsistent with the endpoint of the integration.FeynmanKac.TEqualsToutException- is thrown if during the integration process the actual integration time and the end time of the integration are identical.FeynmanKac.InitialConstraintsException- is thrown if at the initial integration point some of the constraints are inconsistent.FeynmanKac.ConstraintsInconsistentException- is thrown if during the integration process the constraints for the actual time point and given stepsize are inconsistent.SingularMatrixException- is thrown if one of the matrices used outside the integrator is singular.FeynmanKac.BoundaryInconsistentException- is thrown if the boundary conditions are inconsistent.
-
getAbsoluteErrorTolerances
public double[] getAbsoluteErrorTolerances()
Returns absolute error tolerances.- Returns:
- a
doublearray of length3*xGrid.lengthcontaining absolute error tolerances for the solutions.
-
getGaussLegendreDegree
public int getGaussLegendreDegree()
Returns the number of quadrature points used in the Gauss-Legendre quadrature formula.- Returns:
- an
int, the degree of the polynomial used in the Gauss-Legendre quadrature.
-
getInitialStepsize
public double getInitialStepsize()
Returns the starting step size for the integration.- Returns:
- a
double, the starting step size used in the integrator.
-
getMaximumBDFOrder
public int getMaximumBDFOrder()
Returns the maximum order of the BDF formulas.- Returns:
- an
int, the maximum order of the backward differentiation formulas used in the integrator.
-
getMaximumStepsize
public double getMaximumStepsize()
Returns the maximum internal step size used by the integrator.- Returns:
- a
double, the maximum internal step size.
-
getMaxSteps
public int getMaxSteps()
Returns the maximum number of internal steps allowed.- Returns:
- an
intspecifying the maximum number of internal steps allowed between each output point of the integration.
-
getRelativeErrorTolerances
public double[] getRelativeErrorTolerances()
Returns relative error tolerances.- Returns:
- a
doublearray of length3*xGrid.lengthcontaining relative error tolerances for the solutions.
-
getSplineCoefficients
public double[][] getSplineCoefficients()
Returns the coefficients of the Hermite quintic splines that represent an approximate solution of the Feynman-Kac PDE.- Returns:
- a
doublearray of dimension(tGrid.length+1) by (3*xGrid.length)containing the coefficients of the Hermite quintic spline representation of the approximate solution for the Feynman-Kac PDE at time points0, tGrid[0],...,tGrid[tGrid.length-1]. SettingntGrid = tGrid.lengthandnxGrid = xGrid.lengththe approximate solution is given by
The representation for the initial data at![f(x,t) = sum_{j=0}^{3*text{nxGrid}-1}y_{ij}beta_j(x) ; mbox{for} ;
t=text{tGrid}[i-1], i=1,ldots,text{ntGrid}.](eqn_1328.png)
t=0is
The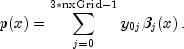
(ntGrid+1) by (3*nxGrid)matrix
is stored row-wise in the returned array.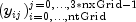
-
getSplineCoefficientsPrime
public double[][] getSplineCoefficientsPrime()
Returns the first derivatives of the Hermite quintic spline coefficients that represent an approximate solution of the Feynman-Kac PDE.- Returns:
- a
doublearray of dimension(tGrid.length+1) by (3*xGrid.length)containing the first derivatives (in time) of the coefficients of the Hermite quintic spline representation of the approximate solution for the Feynman-Kac PDE at time points0, tGrid[0],...,tGrid[tGrid.length-1]. The approximate solution itself is given by
and![f_t(x,bar{t}) = sum_{j=0}^{3*text{nxGrid}-1}y_{ij}' beta_j(x) quad
mbox{for} ; bar{t} = text{tGrid}[i-1], i=1,ldots,text{ntGrid},](eqn_1331.png)
The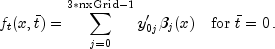
(ntGrid+1) by (3*nxGrid)matrix
is stored row-wise in the returned array.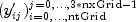
-
getSplineValue
public double[] getSplineValue(double[] evaluationPoints, double[] coefficients, int ideriv)Evaluates for time value 0 or a time value in tGrid the derivative of the Hermite quintic spline interpolant at evaluation points within the range ofxGrid.- Parameters:
evaluationPoints- adoublearray containing the points inx-direction at which the Hermite quintic spline representing the approximate solution to the Feynman-Kac PDE or one of its derivatives is to be evaluated. It is required that all elements in arrayevaluationPointsare greater than or equal toxGrid[0]and less than or equal toxGrid[xGrid.length-1].coefficients- adoublearray of length3*xGrid.lengthcontaining the coefficients of the Hermite quintic spline representing the approximate solution f or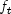 to the Feynman-Kac PDE. These
coefficients are the rows of the arrays
to the Feynman-Kac PDE. These
coefficients are the rows of the arrays splineCoeffsandsplineCoeffsPrimereturned by methodsgetSplineCoefficientsandgetSplineCoefficientsPrime. If the user wants to compute approximate solutions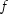 or
or
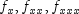 to the Feynman-Kac PDE
at time point
to the Feynman-Kac PDE
at time point 0, one must assign rowsplineCoeffs[0]to arraycoefficients. If the user wants to compute these approximate solutions for time pointst=tGrid[i], i=0,...,tGrid.length-1, one must assign rowsplineCoeffs[i+1]to arraycoefficients. The same reasoning applies to the computation of approximate solutions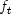 and
and 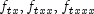 and assignment of rows of array
and assignment of rows of array getSplineCoefficientsPrimeto arraycoefficients.ideriv- anintspecifying the derivative to be computed. It must be 0, 1, 2 or 3.- Returns:
- a
doublearray containing the derivative of orderiderivof the Hermite quintic spline representing the approximate solution f or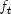 to the Feynman Kac PDE at
to the Feynman Kac PDE at evaluationPoints. Ifideriv=0, then the spline values are returned. Ifideriv=1, then the first derivative is returned, etc.
-
getStepControlMethod
public int getStepControlMethod()
Returns the step control method used in the integration of the Feynman-Kac PDE.- Returns:
- an
intscalar specifying which step control method to be used.Return Value Description METHOD_OF_SOEDERLINDMethod of Soederlind METHOD_OF_PETZOLDMethod from the original Petzold code DASSL
-
getTimeBarrier
public double getTimeBarrier()
Returns the barrier set for integration in the time direction.- Returns:
- a
double, the time point beyond which the integrator should not integrate.
-
setAbsoluteErrorTolerances
public void setAbsoluteErrorTolerances(double atol)
Sets the absolute error tolerances.- Parameters:
atol- adoublescalar specifying the absolute error tolerances for the row-wise solutions returned by methodgetSplineCoefficients. The tolerance valueatolis applied to all3*xGrid.lengthsolution components.atolmust be greater than or equal to zero. Also, not all entries inatolandrtolare allowed to be equal to 0 simultaneously. Default value is 1.0e-5 for each solution component.
-
setAbsoluteErrorTolerances
public void setAbsoluteErrorTolerances(double[] atol)
Sets the absolute error tolerances.- Parameters:
atol- adoublearray of length3*xGrid.lengthspecifying the absolute error tolerances for the row-wise solutions returned by methodgetSplineCoefficients. All entries inatolmust be greater than or equal to zero. Also, not all entries inatolandrtolare allowed to be equal to 0 simultaneously. Default value is 1.0e-5 for each solution component.
-
setForcingTerm
public void setForcingTerm(FeynmanKac.ForcingTerm forceTerm)
Sets the user-supplied method that computes approximations to the forcing term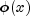 and its derivative
and its derivative 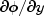 used in the FeynmanKac PDE.
used in the FeynmanKac PDE.- Parameters:
forceTerm- aForcingTerminterface specifying the user defined function used for computation of the forcing term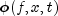 and its derivative
and its derivative
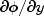 . If this
member function is not called it is assumed that
. If this
member function is not called it is assumed that
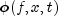 is identically zero.
is identically zero.
-
setGaussLegendreDegree
public void setGaussLegendreDegree(int degree)
Sets the number of quadrature points used in the Gauss-Legendre quadrature formula.- Parameters:
degree- anint, the degree of the polynomial used in the Gauss-Legendre quadrature. It is required thatdegreeis greater than or equal to 6. The default value is 6.
-
setInitialData
public void setInitialData(FeynmanKac.InitialData initData)
Sets the user-supplied method for adjustment of initial data or as an opportunity for output during the integration steps.- Parameters:
initData- anInitialDataobject specifying the user-defined function for adjustment of initial data or the object can be used as an opportunity for output during the integration steps. If this member function is not called, no adjustment of initial data or output during the integration steps is done.
-
setInitialStepsize
public void setInitialStepsize(double initStepsize)
Sets the starting stepsize for the integration.- Parameters:
initStepsize- adouble, the starting stepsize used by the integrator. Must be less than zero since the integration is internally done fromt=0tot=tGrid[tGrid.length-1]in a negative direction. The default isinitStepsize = -1.1102230246252e-16.
-
setMaximumBDFOrder
public void setMaximumBDFOrder(int maxBDFOrder)
Sets the maximum order of the BDF formulas.- Parameters:
maxBDFOrder- anintspecifying the maximum order of the backward differentiation formulas used in the integrator. It is required thatmaxBDFOrderis greater than zero and smaller than 6. The default ismaxBDFOrder = 5.
-
setMaximumStepsize
public void setMaximumStepsize(double maximumStepsize)
Sets the maximum internal step size used by the integrator.- Parameters:
maximumStepsize- a positive scalar of typedouble, the maximum internal step size. Default value isDouble.MAX_VALUE, the largest possible machine number.
-
setMaxSteps
public void setMaxSteps(int maxSteps)
Sets the maximum number of internal steps allowed.- Parameters:
maxSteps- anintspecifying the maximum number of internal steps allowed between each output point of the integration.maxStepsmust be positive. The default value is 500000.
-
setRelativeErrorTolerances
public void setRelativeErrorTolerances(double rtol)
Sets the relative error tolerances.- Parameters:
rtol- adoublescalar specifying the relative error tolerances for the solution. The tolerance valuertolis applied to all3*xGrid.lengthsolution components.rtolmust be greater than or equal to zero. Also, not all entries inatolandrtolare allowed to be equal to 0 simultaneously. Default value is 1.0e-5 for each solution component.
-
setRelativeErrorTolerances
public void setRelativeErrorTolerances(double[] rtol)
Sets the relative error tolerances.- Parameters:
rtol- adoublearray of length3*xGrid.lengthspecifying the relative error tolerances for the solution. All entries inrtolmust be greater than or equal to zero. Also, not all entries inatolandrtolare allowed to be equal to 0 simultaneously. Default value is 1.0e-5 for each solution component.
-
setStepControlMethod
public void setStepControlMethod(int stepControlMethod)
Sets the step control method used in the integration of the Feynman-Kac PDE.- Parameters:
stepControlMethod- anintscalar specifying the step control method to be used in the integration. If this member function is not calledstepControlMethodis set toMETHOD_OF_SOEDERLINDby default.stepControlMethodDescription METHOD_OF_SOEDERLINDUse method of Soederlind. METHOD_OF_PETZOLDUse method from the original Petzold code DASSL.
-
setTimeBarrier
public void setTimeBarrier(double timeBarrier)
Sets a barrier for the integration in the time direction.- Parameters:
timeBarrier- adouble, controls whether the integrator should integrate in the time direction beyond a special point,timeBarrier, and then interpolate to get the Hermite quintic spline coefficients and its derivatives at the points intGrid. It is required thattimeBarrierbe greater than or equal totGrid[tGrid.length-1]. The default istimeBarrier = tGrid[tGrid.length-1].
-
setTimeDependence
public void setTimeDependence(boolean[] timeFlag)
Sets the time dependence of the coefficients, boundary conditions and function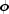 in the Feynman Kac equation.
in the Feynman Kac equation.- Parameters:
timeFlag- abooleanvector of length 7 indicating time dependencies in the Feynman-Kac PDE.Index Time dependency of 0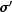
1
2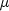
3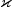
4Left boundary conditions 5Right boundary conditions 6
timeFlag[i] = trueindicates that the associated value is time-dependent,timeFlag[i] = falseindicates that the associated value is not time-dependent. By default,timeFlag[i] = falsefor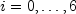 .
.
-
-